Question ouverte et Polynome
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
justinedu35
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Avr 2007, 18:48
-
 par justinedu35 » 15 Avr 2008, 08:18
par justinedu35 » 15 Avr 2008, 08:18
[CENTER]Salut à tous,j'ai une petite question de dm que j'ai un peu de mal à rédoudre.
J'ai soit p = x ^4 +1
Et je doisfactoriser P ss forme d'1 produit de coefficient réels[/CENTER]
ALors tout d'abord je sais qu'un polynome de degré n admet n racines réelles ou imaginaires, donc ici normalement 4 racines possibles.
Et aussi comme les coeff sont réels alors les racines imaginaires sont conjugués mais comment retrouver les ecritures par un calcul?
-
Benjamin
- Membre Complexe
- Messages: 2337
- Enregistré le: 14 Avr 2008, 10:00
-
 par Benjamin » 15 Avr 2008, 08:37
par Benjamin » 15 Avr 2008, 08:37
Salut,
Une petite astuce générale quand tu as des polynômes de degré 4 dont seul les puissances présentes sont les puissances paires. Un changement de variable X=x² s'avère utile. Si tu n'arrives toujours pas à résoudre, fais moi signe ;)
A plus,

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 15 Avr 2008, 08:37
par fatal_error » 15 Avr 2008, 08:37
Salut,
A priori, il faut factoriser dans IC, et apres comme tu l'as dis, developper les facteurs de termes (ca se dit?) conjugués.
Donc pour factoriser je pense que tu sais faire.
t'obties
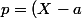(X-b)(X-\overline{a})(X-\overline{b}))
ou
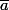
et
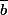
sont les conjugués de a et b.
apres tu developpes
(X-\overline{a}))
pareil pour b, qui te donneront de trinomes de second degré à coefficients réels.
la vie est une fête

-
justinedu35
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Avr 2007, 18:48
-
 par justinedu35 » 15 Avr 2008, 08:43
par justinedu35 » 15 Avr 2008, 08:43
justement je ne sais plus factoriser... :hum:
-
justinedu35
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Avr 2007, 18:48
-
 par justinedu35 » 15 Avr 2008, 08:50
par justinedu35 » 15 Avr 2008, 08:50
avec le changement de variable je trouve z1=i ou z2=-i
-
Benjamin
- Membre Complexe
- Messages: 2337
- Enregistré le: 14 Avr 2008, 10:00
-
 par Benjamin » 15 Avr 2008, 08:51
par Benjamin » 15 Avr 2008, 08:51
Re,
Utilise la méthode que j'ai fourni plutôt que la factorisation. Changement de variables, ça marche bien. Ensuite, pour factoriser, il faut fonctionner à l'envers. Tu pars de la forme factorisée et tu développes. A toi de choisir la méthode qui te convient le mieux ;)
A plus,
-
justinedu35
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Avr 2007, 18:48
-
 par justinedu35 » 15 Avr 2008, 08:56
par justinedu35 » 15 Avr 2008, 08:56
Donc quand jeffectue le changement de variable j'ai z1=i et z2= -i
mais après je peux factoriser X²+1= (x-i)(x+i)
mais bon ça c quand jai effectué le changement de variable.
alors si X=x²
c'estequivalent à x²=z1
x²=i
x=+ou- racine de i
ou x²=z2
x²=-i
x=+ou - racine de -1
C'est ennuyeux ces racines
-
Benjamin
- Membre Complexe
- Messages: 2337
- Enregistré le: 14 Avr 2008, 10:00
-
 par Benjamin » 15 Avr 2008, 09:01
par Benjamin » 15 Avr 2008, 09:01
Re,
Oui, ces racines peuvent sembler ennuyeuse. Une autre indication donc, écris i et -i sont forme exponentiel. Et vois la fonction racine carré comme une mise à la puissance. Quelle est la valeur de cette puissance ?
A plus,

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 15 Avr 2008, 09:04
par fatal_error » 15 Avr 2008, 09:04
[Hop la, deja entamé par benjamin631, désolé]
PS2:sinon tu peux remarquer que les racines de X^4+1 sont les solutions de

or
}=-1)
D'ou
)
pour k=1..4 (4 racines), mais bon pour la derniere on a pas trop vu ca en terminale...
la vie est une fête

-
justinedu35
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Avr 2007, 18:48
-
 par justinedu35 » 15 Avr 2008, 09:04
par justinedu35 » 15 Avr 2008, 09:04
z1= e(ipi/2) et z2=e(3ipi/2)
-
justinedu35
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Avr 2007, 18:48
-
 par justinedu35 » 15 Avr 2008, 09:08
par justinedu35 » 15 Avr 2008, 09:08
ok j'ai mes valeurs de i maispour la fonction racine je ne vois pas du tout sa va me donner +ou- racine de (e(ipi/2) ou +-racine de e(3ipi/2))
-
justinedu35
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Avr 2007, 18:48
-
 par justinedu35 » 15 Avr 2008, 09:23
par justinedu35 » 15 Avr 2008, 09:23
Pouvez vous m'aider pour la suite jsuis coincée aux exponentielles
-
justinedu35
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Avr 2007, 18:48
-
 par justinedu35 » 15 Avr 2008, 09:28
par justinedu35 » 15 Avr 2008, 09:28
je trouve z1= +ou - e (ipi/4) et z2= + ou - e (3ipi/4) et ensuite?
-
Youcef
- Membre Naturel
- Messages: 60
- Enregistré le: 22 Mar 2008, 14:19
-
 par Youcef » 15 Avr 2008, 09:30
par Youcef » 15 Avr 2008, 09:30
Salut ..
et bein tes réponses sont bonnes .. maintenant tu obtient bien 4 racines non?? alors qu'est ce que tu vas en faire ??
-
justinedu35
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Avr 2007, 18:48
-
 par justinedu35 » 15 Avr 2008, 09:35
par justinedu35 » 15 Avr 2008, 09:35
ben normalement on factorise par a (z-z1)(z-z2) pour un trinome du second degré mais làc different ça pourrait faire
(x+eipi/4)(x-eipi/4)(x+eipi/4)(x-eipi/4) MAis les coeff sont reels? ya pas moyen de simplifier e ipi/4?
-
justinedu35
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Avr 2007, 18:48
-
 par justinedu35 » 15 Avr 2008, 09:45
par justinedu35 » 15 Avr 2008, 09:45
Alors c'est cela?
-
Youcef
- Membre Naturel
- Messages: 60
- Enregistré le: 22 Mar 2008, 14:19
-
 par Youcef » 15 Avr 2008, 09:50
par Youcef » 15 Avr 2008, 09:50
ce polynôme n'admet pas de racines dans R . Donc la seul factorisation est celle que tu as trouvé .
Voila voila , bonne journée !
-
justinedu35
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Avr 2007, 18:48
-
 par justinedu35 » 15 Avr 2008, 09:57
par justinedu35 » 15 Avr 2008, 09:57
Donc comme on me demande de factoriser P sous la forme d'un prduit de polynomes à coefficients réels, c'est que c'est pas possible?
-
Youcef
- Membre Naturel
- Messages: 60
- Enregistré le: 22 Mar 2008, 14:19
-
 par Youcef » 15 Avr 2008, 10:06
par Youcef » 15 Avr 2008, 10:06
Re ,
Moi j'ai juste suivi la fin de la discussion, mais je viens de relire ton premier com.
il y a une réponse dans R , je te la prépare tout de suite !
Alors : X^4+1= X^4+2x^2+1-2x^2
= (x^2+1)^2 -2x^2 = (x^2+1)^2 -(x*racine(2))^2
la c'est une identité remarquable , tu sais ce qui te reste a faire !
Quand on demande de factoriser dans R, on doit trouver un produit de polynômes de degré 2 ou 1 . Or la tu arrive a 2 polynome irreductible , donc tu pas pas aller plus loin dans R .
T'as compris ?
-
justinedu35
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Avr 2007, 18:48
-
 par justinedu35 » 15 Avr 2008, 10:11
par justinedu35 » 15 Avr 2008, 10:11
Donc comme on me demande de factoriser P sous la forme d'un prduit de polynomes à coefficients réels, c'est que c'est pas possible?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
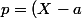(X-b)(X-\overline{a})(X-\overline{b})) ou
ou 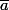 et
et 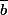 sont les conjugués de a et b.
sont les conjugués de a et b.(X-\overline{a})) pareil pour b, qui te donneront de trinomes de second degré à coefficients réels.
pareil pour b, qui te donneront de trinomes de second degré à coefficients réels.
