Réunion disjointe dans C

par **Anonyme** » 02 Nov 2005, 15:06

Bonjour je suis en PCSI,
Soit Un le groupe multiplicatif des racines niemes de l'unité.
Soit Pn le sous-ensemble multiplicatif des racines primitives niemes de l'unité.

Soit p un nombre premiers >0
Je dois démontrer que Up est la réunion disjointe de U(p^(a-1)) et P(p^a)
avec a entier naturel >0

Je ne vois pas comment prouver que c'est une réunion disjointe.

Je pense qu'il faut montrer qu'une racine ième qui n'est pas primitive est en fait ième
mais je n'y arrive pas
merci d'avance..

par **Tchou** » 02 Nov 2005, 15:43

Mdr ! tu serais pa a gustave effeil toi ???
ahahahhahahaha
toi aussi ten chi ! c ça kest bon

tien c bizarre ! on a le meme travail ;)

par **Anonyme** » 02 Nov 2005, 15:48

Jsuis dégouté je m'attendais à une réponse !!
Lol
Attention Tastou rôde dans les parages !!

par **Anonyme** » 02 Nov 2005, 15:48

jsuis dégouté je m'attendais à une réponse et oui j'en chi !!!!!

par **Anonyme** » 02 Nov 2005, 15:58

t'as pas une idée sur la question lol ?

par **Tchou** » 02 Nov 2005, 16:00

Bah non c ça le truc c ke jen chi aussi pour la meme question !
ta pa msn ça sera plu simple pour eclaircir la mathematisation de ce souci ?
voila mon msn, ajoute moi si ta aussi
tchou@hotmail.fr

par **LN1** » 02 Nov 2005, 16:00

Bonjour,

il y a une erreur dans ton énoncé:
il faut montrer que

(et non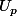

)
avec

pour démontrer que les ensembles sont disjoints, il suffit de prouver qu'aucun élément de

n'est dans

. Ce qui n'est pas très difficile.
en effet une racine primitive doit engendrer toutes les autres. C'est à dire que

. Or si z appartient à

, l'ensemble

ne contient que

éléments.

pour démontrer que l'union donne

, il faut démontrer que toute racine non primitive est bien dans

. Cela se fait en regardant le groupe multiplicatif

où z est une racine non primitive
Ce groupe multiplicatif est un sous-groupe de

distinct de

car z n'est pas une racine primitive. Son cardinal m est donc un diviseur de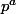

différent de

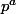, c'est donc un diviseur de

(car p est un nombre premier). On sait donc que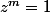

et, puisque

est un multiple de m,

donc z appartient à

par **Tchou** » 02 Nov 2005, 16:11

Cimer LN1 t un amour
dit tu pourrai nous aidé aussi pour la kestion sur " LE CARDINAL DES RACINES PRIMITIVES "

merci davance !

bisouz

par **LN1** » 02 Nov 2005, 16:16

pardon??
je ne comprends que le français pas le SMS, ni le verlan :we:

par **Tchou** » 02 Nov 2005, 16:28

Excuse moi, je te disais juste merci

et puis il y a une autre question sur le cardinal des racines primitives où en fait on cherche a connaitre le cardinal des racines primitives p-ieme, c'est a dire : Card Pp ainsi que la somme des éléments de Pp.

As tu un fil conducteur ( mais pa isolant ) pour nous aider quelque peut dans notre quete mathematique ?

Merci d'avance

par **LN1** » 02 Nov 2005, 16:41

Tu as tout dans l'égalité démontrée plus haut

Tu connais le cardinal de

? (combien y a-t-il de racines nième de l'unité ?)
tu sais que

et tu sais que l'union est disjointe donc

donc ....

tu connais la somme des éléments de

?(somme des termes d'une suite géométrique ?)
la somme des termes de

qui vaut ..... se décompose en la somme des termes de

qui vaut .... et la somme des termes de

qui vaut donc .....

rem : s'il s'agit uniquemen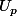t de

et de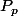

remplace donc a par 1

par **Tchou** » 02 Nov 2005, 16:55

Non c bon j'ais rien dit !!!

par **Zeitblom** » 02 Nov 2005, 16:58

Le cardinal cherché vaut

où

est l'indicatrice d'Euler, et la somme des racines primitives vaut

où µ est la fonction de Moebius. Je vous laisse chercher pourquoi...

Réunion disjointe dans C

réunion disjointe dans C

Qui est en ligne