Réunion intersection

[MoRBT]

Bonjour,

Je n'arrive pas à comprendre la construction des deux ensembles et (voir s'il n y a pas de faute dans l'énoncé) dans l'exo suivant:

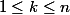
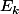
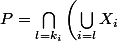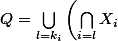Soient ensembles quelconques, un entier tel que . On note l’ensemble des parties à éléments de . et , donc est l’intersection de toutes les réunions à et la réunion de toutes les intersections à des ensembles . Montrer que :

a) 1) si , alors inclus dans

Je vous remercie par avance.

[girdav]

Bonjour,
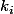
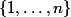
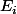
on ne sait pas qui est . Je pense que , c'est-à-dire que est dans si et seulement si dès que l'on prend un ensemble à éléments contenu dans se trouve dans l'un des pour un de cet ensemble.

[MoRBT]

Merci Mr. girdav pour l'explication,

Il y a plus de 3 heures que j'essaye de trouver une solution mais je n'ai pas trouvé l'idée.


Je vous remercie pour votre aide.

[girdav]

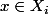
On prend x dans P, et on cherche un sous-ensemble de {1,...,n} contenant k éléments tel que x\in X_i pour tout i dans cet ensemble. On peut noter J l'ensemble des indices i tels que . Il faut montrer que le cardinal de J est au moins k. S'il est strictement plus petit, contient un ensemble à éléments et on se sert du fait que pour aboutir à une contradiction.

[MoRBT]

C'est bon,

Merci beaucoup beaucoup Girdav.