Réunion de cercles dans le plan

[fahr451]

Un résultat (dont je connais la preuve) assez joli que je vous propose:
Le plan (euclidien) n 'est pas réunion de cercles ( non réduits à des points) disjoints.

[Imod]

Une question subsidiaire , et l'espace ?

Imod

[nuage]

:++:

Une question subsidiaire , et l'espace ?

Imod

:++:
Ce qui est un résultat beaucoup plus beau (et qui m'a toujours étonné).

[tize]

Un résultat (dont je connais la preuve) assez joli que je vous propose:
Le plan (euclidien) n 'est pas réunion de cercles ( non réduits à des points) disjoints.

Supposons : des cercles disjoints du plan qui le recouvre. Quitte à utiliser une homothétie, on peut supposer qu'un de ces cercles est centré en 0 et de rayon 1. On appelle ce cercle. Le centre de appartient à un des cercles qui recouvre le plan mais son rayon doit être inférieur ou 1/2 (sinon les deux cercles se recoupent).
Par récurrence on construit donc des cercles de rayon inférieur à avec est dans l'intérieur du cercle .
La suite des disques fermés correspondant aux cercles est donc une suite décroissante de fermés non vide dont le diamètre tend vers 0 et comme est complet l'intersection de tous ces disques est égal à un singleton qui lui ne peut appartenir à aucun des cercles (de rayon >0) sinon il recoupe un des .

[fahr451]

absolument tize

j'ai la même preuve pour cette question qui date déjà d'un moment

[tize]

Par contre pour l'espace, la remarque de Nuage me fait penser que c'est possible mais je dois avouer que là j'ai encore besoin de beaucoup de réflexion...

[Imod]

Un petit indice pour tize .

On peut commencer par montrer que toute sphère privée de deux points est partitionnable ( ça ne doit pas figurer dans le dico ) avec des cercles .

Imod

[yos]

sphère ou boule?

[tize]

Salut Yos,
je pense que c'est sphère même si j'ai beaucoup de mal à le décrire tout en le visualisant assez bien...avec des cercles sur cette sphère de plus en plus petits qui se terminent par un cercle de rayon nul justement là on l'on a enlevé les deux points en question.

[Imod]

Je parlais bien de sphère , même si ce soir j'ai un peu les boules ( je ne le dis pas trop fort , les murs ont des oreilles ) .

Imod

[tize]

Je parlais bien de sphère , même si ce soir j'ai un peu les boules ( je ne le dis pas trop fort , les murs ont des oreilles ) .

Imod

Même chose pour moi :mur: :mur: mais de toute manière ces murs ci n'auront bientôt même plus besoin de leurs oreilles, d'autre se chargeront d'écouter.

[yos]

Oui pour une sphère c'est assez évident. Moi j'avais réussi à paver un tore (et sans enlever de point). Bon c'est pas révolutionnaire, je reconnais, mais bon. En tout cas, mon intuition semblait la bonne : ça le fait pour l'espace non?
Pour les boules, je ressens la même chose que vous deux.

[Imod]

Pour l'espace c'est possible et l'indication "sphère privée de deux points" n'est pas sans intérêt .

Imod

PS : Je donnerais un peu plus de détails demain si personne ne trouve d'ici là .

[Imod]

Un nouvel indice :

On choisit un point O de l'espace et on note S l'ensemble des sphères de centre O . Il faut trouver un ensemble C de cercles disjoints dont l'un passe par O et tel que toute sphère de S intersecte C en exactement deux points .

Imod

[yos]

Je suis ton indication Imod :
Prenons un cercle passant par O, de rayon R. Il coupe toute sphère de centre O et de rayon < 2R en exactement deux points.
Quant à la sphère S de centre O et de rayon 2R, elle touche en un seul point A. On choisit un autre point B sur cette sphère et un cercle de rayon R, tangent extérieurement à S en B. Les sphères de rayon 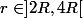coupent selon deux points. etc.

Reste à voir que les sphères privées de deux points sont pavables par des cercles. J'ai dit plus haut que c'est évident, mais je songeais au cas où les deux points sont diamétralement opposés. Je réfléchis au cas général.

[Imod]

Prenons un cercle de centre O, de rayon R.

Tu veux dire passant par O je suppose ?

Imod

[yos]

Merci je rectifie.

[yos]

:id: Ouais j'ai eu la même idée que Yos. Bon c'est moins bien formulé forcément.

Et une minute avant moi!
Ta rédaction est très bien.

[Imod]

Les grands esprits se rencontrent , une illustration :



Imod

[yos]

Je vois bien comment paver une sphère moins deux points, mais j'ai une pauvre explication. Les sections planes que j'utilise sont mal caractérisées. Je vais améliorer ça, à moins que quelqu'un ne le fasse.

En tout cas c'est un beau problème.
Est-ce ta solution Imod ou est-ce un classique?