bonjour à tous
je vais mettre a votre disposition un exercice que je n'ai pas bien compris
trouver une droite qui soit à la fois tangente et normale à la courbe
x=3t².
y=2t^3.
merci pour votre suggestions :zen:
Petit exo déconseillé pour les novices!!!!
9 messages
- Page 1 sur 1
Au pooint de paramètre t (non nul), la tangente a pour vecteur directeur ) soit
soit ) donc pour équation
donc pour équation =y-2t^3) , ce qui est équivalent à
, ce qui est équivalent à 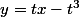 . D'autre part, un vecteur orthogonal à
. D'autre part, un vecteur orthogonal à ) est
est ) , c'est le vecteur tangent à la courbe au point de paramètre
, c'est le vecteur tangent à la courbe au point de paramètre 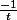 . Reste à voir pour quelle valeur de t le point de paramètre
. Reste à voir pour quelle valeur de t le point de paramètre 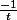 est sur la courbe.
est sur la courbe.
Pour paraphraser Galt
la droite (d) est tangente à la courbe en M(t) donc son vecteur directeur est u(1 , t)
la droite (d) est normale à la courbe en N(t') donc son vecteur directeur est u(1 ; -1/t')
donc t' = -1/t
il faut maintenant trouver t tel que la tangente (d) à la courbe en M(t) passe par le point N(-1/t)
(d) :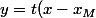 + y_M)
(d) :+ 2t^3)
N(-1/t) de coordonnées ( ) appartient à (d) ssi
) appartient à (d) ssi
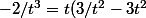 + 2t^3)
après avoir mulitplié par t^3, tu obtiens une équation polynomiale en t qu'il te suffit de résoudre en posant T = t², puis en cherchant des racines evidentes du polynôme de degré 3 que tu vas obtenir
bon courage
la droite (d) est tangente à la courbe en M(t) donc son vecteur directeur est u(1 , t)
la droite (d) est normale à la courbe en N(t') donc son vecteur directeur est u(1 ; -1/t')
donc t' = -1/t
il faut maintenant trouver t tel que la tangente (d) à la courbe en M(t) passe par le point N(-1/t)
(d) :
(d) :
N(-1/t) de coordonnées (
après avoir mulitplié par t^3, tu obtiens une équation polynomiale en t qu'il te suffit de résoudre en posant T = t², puis en cherchant des racines evidentes du polynôme de degré 3 que tu vas obtenir
bon courage
sauf erreur de ma part
l'équation s'écrit
-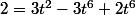
équivalent à
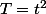
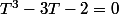
équivalent à
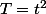
(T+1)^2 = 0)
équivalent à
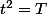
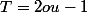
équivalent à
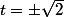
Il y a donc deux droites verifiant ces conditions
(d1) :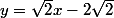
tangente à (C) au point)
normale à (C) au point)
(d2 :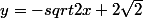
tangente à (C) au point)
normale à (C) au point)
l'existence de deux droites provient de l'axe de symétrie de la courbe symétrique par rapport à (Ox)
l'équation s'écrit
-
équivalent à
équivalent à
équivalent à
équivalent à
Il y a donc deux droites verifiant ces conditions
(d1) :
tangente à (C) au point
normale à (C) au point
(d2 :
tangente à (C) au point
normale à (C) au point
l'existence de deux droites provient de l'axe de symétrie de la courbe symétrique par rapport à (Ox)
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
