En général, je comprends bien la matière, mais je suis embêté lorsque vient le temps de prouver des énoncés. Certains semblent évidents, mais de là à les démonter....
Donc voilà:
Quel(s) énoncé(s) sont vrais parmi les suivants? (montrez les détails).
1) 1 + i = [1 + (i^(m)/m)]^m
2) 1 + i = e^-;)
3) ;) > i
4) i^(4) = 4(e^;) - 1)
Merci d'avance!
NB: Les caractères entre parenthèses placés en exposant aux nos 1 et 4 ne correspondent pas à des exposant, mais bien à des périodes.
Math. financières
10 messages
- Page 1 sur 1
ElTopo a écrit:En général, je comprends bien la matière, mais je suis embêté lorsque vient le temps de prouver des énoncés. Certains semblent évidents, mais de là à les démonter....
Donc voilà:
Quel(s) énoncé(s) sont vrais parmi les suivants? (montrez les détails).
1) 1 + i = [1 + (i^(m)/m)]^m
2) 1 + i = e^-;)
3)> i
4) i^(4) = 4(e^;) - 1)
Merci d'avance!
NB: Les caractères entre parenthèses placés en exposant aux nos 1 et 4 ne correspondent pas à des exposant, mais bien à des périodes.
Nicolas_75 a écrit:Pour ma part, je ne connais pas assez les mathématiques financières.
Il me faudrait la définition de ces grandeurs.
Ben oui ! Une définition mathématique aiderait, ou un exemple du type :
Pour un certain prêt, on a i=..., delta=...,m=..., après on pourra retrouver ses petits (peut-être).
Répondre "Le
Par contre je peux préciser un peu les choses :
Si on a un taux nominal (je pense qu'on appelle aussi cela TEG, mais l'affectation d'un terme scientifique à cette quantité ne lui donne pas le droit de cité parmi les grandeurs respectables : elle ne correspond absolument à rien) de 6% l'an, cela signifie que le taux d'intérêt mensuel est de 6/12 soit 0,5% (t=0.005) (ce qui par parenthèse est un véritable scandale).
Alors le taux réel annuel est de (1+t)^12-1 : il porte un nom depuis quelques années (mais j'ai oublié comment il s'appelle), enfin : c'est la seule quantité qui puisse réellement désigner le véritable taux d'intérêt d'un prêt rapporté à l'année. Il est toujours supérieur au taux nominal : c'est la raison pour laquelle les banquiers lui préfèrent le TEG qui a l'avantage de minimiser le taux face à leur clients emprunteurs.
Voici mon exemple : un prêt de C=100000 euros au taux nominal de 6% (taux réel mensuel t=0,005, taux réel annuel (1+t)^12-1=6,167781186 %, à rembourser en n=180 mensualités constantes de :
(je sais bien qu'on arrondit au centime supérieur, mais j'ai laissé pas mal de décimales pour que tu puisses bien vérifier ma formule)
Donc, pour ce cas précis, quel est la valeur de ton
Désolé, si je ne suis pas très clair. C'est que j'ai un peu de misère à comprendre moi-même.
Je vais tenter de vous éclairer en énonçant quelques définitions:
-Si l'intérêt est capitalisé m fois par période (avec m *;) 1) et que le taux d'intérêt pour chacun de ces m ièmes de période est i^(m) / m, alors nous disons que le taux nominal d'intérêt est i^(m). (Ça rejoint un peu ce que tu disais Chimerade)
** i^(m) i^m (Le premier cas dénote le taux nominal, alors que le second dénote i à la puissance m).
i^m (Le premier cas dénote le taux nominal, alors que le second dénote i à la puissance m).
-De façon plus générale, le taux effetif d'intérêt i équivalent au taux nominal d'intérêt i^(m), correspondant à une situation pour laquelle l'intérêt est capitalisé m fois par période, est obtenu en considérant la valeur accumulée après un an lorsque 1$ est investi aux taux i et i^(m). Cette valeur accumulée est:
(1 + i) = (1 + (i^(m) / m))^m
EXEMPLE: Si 7000$ est placé au taux nominal d'intérêt de 5% capitalisé trimestriellement, i.e. le taux nominal est i^(4) = 5%. Quelle sera la valeur accumulée après 30 mois? L'intérêt aura été capitalisé 30 / 3 = 10 fois et ainsi la valeur accumulée sera:
7000 (1 + (0.05 / 4))^10 = 7925.90$
-Si A(t) est la fonction d'accumulation d'un placement au temps t et dans lequel aucune principal n'est ajouté ni retiré (i.e. seulement l'intérêt fait que le fonds croît), alors le taux instantané de l'intérêt (ou force de l'intérêt), noté t, est défini par la formule:
t, est défini par la formule:
 t = A'(t) / A(t)
t = A'(t) / A(t)
De même, la fonction de capitalisation a(t) du placement est définie ainsi:
 t = a'(t) / a(t)
t = a'(t) / a(t)
-Dans la cas de l'intérêt composé, si le taux d'intérêt est i, alors la fonction de capitalisation est a(t) = (1 + it)
Dans ce cas, nous obtenons que le taux instantané est:
 t = i / (1 + it) si t *;) 0
t = i / (1 + it) si t *;) 0
-Si le taux instantané d'intérêt t est constant
t est constant  pour tout t *;) 0, i.e.
pour tout t *;) 0, i.e.  t =
t =  pour tout t *;) 0, alors la fonction de capitalisation est:
pour tout t *;) 0, alors la fonction de capitalisation est:
a(t) = e^;)t pour tout t *;) 0
Dans ce cas, le taux effectif d'intérêt in pour la n ième période est constant et égal à:
in = e^;) - 1
En notant le taux effectif par i, nous avons 1 + i = e^;).
Conséquemment les équations:
i = e^;) - 1 et = ln(1 + i)
= ln(1 + i)
EXEMPLE:
Dans le cas d'un placement de 25 000$ investi pour 6 ans. Si le placement est rémunéré au taux instantané de 4%, la valeur accumulée sera:
A(6) = A(0) exp ((0,04)x6) = 25 000 exp (0.24) = 31 781.23$
Voilà, j'espère que tout ça vous aura aidé.
Je vais tenter de vous éclairer en énonçant quelques définitions:
-Si l'intérêt est capitalisé m fois par période (avec m *;) 1) et que le taux d'intérêt pour chacun de ces m ièmes de période est i^(m) / m, alors nous disons que le taux nominal d'intérêt est i^(m). (Ça rejoint un peu ce que tu disais Chimerade)
** i^(m)
-De façon plus générale, le taux effetif d'intérêt i équivalent au taux nominal d'intérêt i^(m), correspondant à une situation pour laquelle l'intérêt est capitalisé m fois par période, est obtenu en considérant la valeur accumulée après un an lorsque 1$ est investi aux taux i et i^(m). Cette valeur accumulée est:
(1 + i) = (1 + (i^(m) / m))^m
EXEMPLE: Si 7000$ est placé au taux nominal d'intérêt de 5% capitalisé trimestriellement, i.e. le taux nominal est i^(4) = 5%. Quelle sera la valeur accumulée après 30 mois? L'intérêt aura été capitalisé 30 / 3 = 10 fois et ainsi la valeur accumulée sera:
7000 (1 + (0.05 / 4))^10 = 7925.90$
-Si A(t) est la fonction d'accumulation d'un placement au temps t et dans lequel aucune principal n'est ajouté ni retiré (i.e. seulement l'intérêt fait que le fonds croît), alors le taux instantané de l'intérêt (ou force de l'intérêt), noté
De même, la fonction de capitalisation a(t) du placement est définie ainsi:
-Dans la cas de l'intérêt composé, si le taux d'intérêt est i, alors la fonction de capitalisation est a(t) = (1 + it)
Dans ce cas, nous obtenons que le taux instantané est:
-Si le taux instantané d'intérêt
a(t) = e^;)t pour tout t *;) 0
Dans ce cas, le taux effectif d'intérêt in pour la n ième période est constant et égal à:
in = e^;) - 1
En notant le taux effectif par i, nous avons 1 + i = e^;).
Conséquemment les équations:
i = e^;) - 1 et
EXEMPLE:
Dans le cas d'un placement de 25 000$ investi pour 6 ans. Si le placement est rémunéré au taux instantané de 4%, la valeur accumulée sera:
A(6) = A(0) exp ((0,04)x6) = 25 000 exp (0.24) = 31 781.23$
Voilà, j'espère que tout ça vous aura aidé.
ElTopo a écrit:Est-ce que c'est suffisament clair?
Désolé, je n'ai pas eu le temps aujourd'hui. Ca n'a pas l'air évident... Mais il est trop tard, il faut que j'aille me coucher (je suis sur TU+2 : il est 1 h)
demain, peut-être
P.S. je suis surtout troublé par (m). Ca me paraît bizarre ; enfin, je verrai ca demain
J'avoue que je suis perdu dans ces notations : d'une part il s'agit d'un langage de financier auquel je ne suis guère habitué, d'autre part, je sens à votre accent que vous devez être au Canada, ce qui complique encore les choses, les vocables utilisés de ce côté de l'Atlantique différant parfois de ceux que l'on utilise "par chez vous"...
Je suis déjà troublé par les définitions :
La notation "non mathématique" (d'après vous) (i^m)/m est extrêmement troublante. Si ce n'est pas mathématique, il ne faut pas l'employer dans des formules ! Si ça l'est, il doit bien y avoir une formule compréhensible par un mathématicien qui en donne une définition précise !
Ici aussi, je suis perdu dans le texte, alors que je comprends la formule !
[INDENT]Pour moi, il n'y a qu'un seul taux annuel et toute cette discussion provient des inventions bizarroïdes de mots pour des choses qui ne correspondent à aucune réalité.
Si le taux réel annuel est i, le taux réel mensuel ne peut être autre chose que^{\frac{1}{12}}-1) . Si le taux réel annuel est i le taux réel trimestriel ne peut être autre chose que
. Si le taux réel annuel est i le taux réel trimestriel ne peut être autre chose que ^{\frac{1}{4}}-1) . Inversement, si le taux réel mensuel est j, le taux réel annuel ne peut être autre chose que
. Inversement, si le taux réel mensuel est j, le taux réel annuel ne peut être autre chose que ^{12}-1) .[/INDENT]
.[/INDENT]
A l'époque où nous avions des taux de 12% l'an (je veux dire que les banques affichaient "taux nominal = 12%), on s'apercevait que les calculs étaient parfaitement exacts à condition de prendre des taux mensuels de 1% exactement. Tous les guichetiers des banques soutenaient mordicus que le taux mensuel était le douzième du taux annuel. La raison est que l'utilisation d'une exponentielle dépasse largement les capacités intellectuelles du client moyen et que par suite les banques jugent inutile d'employer comme guichetier un type qui connaît les exponentielles vu que tout ce qu'il dirait ne pourrait être compris par l'homme de la rue ! Donc pour moi, 1% par mois, c'est soit 12,68% par an !
soit 12,68% par an !
Appelons le taux réel par mois,
le taux réel par mois,  le taux réel par bimestre,
le taux réel par bimestre,  le taux réel par trimestre,
le taux réel par trimestre,  le taux réel par semestre etc... Pour recoller avec ta notation où m est le nombre de périodes par an, si l'on s'intéresse au taux par mois, on considère
le taux réel par semestre etc... Pour recoller avec ta notation où m est le nombre de périodes par an, si l'on s'intéresse au taux par mois, on considère  , et toi tu fais m=12. Si l'on s'intéresse au taux par trimestre, j'appelle cela
, et toi tu fais m=12. Si l'on s'intéresse au taux par trimestre, j'appelle cela  et toi tu fais m=4. Donc d'une façon générale, l'intérêt sur k mois correspond à
et toi tu fais m=4. Donc d'une façon générale, l'intérêt sur k mois correspond à 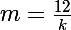
Si je compare ta formule (1 + i) = (1 + (i^(m) / m))^m avec la mienne=(1+i_3)^4) dans le cas de m=4,
dans le cas de m=4,  taux réel par an,
taux réel par an,  taux réel par trimestre, je constate alors que ce que tu appelles (i^(m) / m) (vraiment bizarre comme notation, je ne m'y ferai jamais !), ou, pour fixer les idées, avec m=4, ce que tu appelles (i^(4) / 4) est ce que j'appelle
taux réel par trimestre, je constate alors que ce que tu appelles (i^(m) / m) (vraiment bizarre comme notation, je ne m'y ferai jamais !), ou, pour fixer les idées, avec m=4, ce que tu appelles (i^(4) / 4) est ce que j'appelle  qui est égal donc à :
qui est égal donc à : 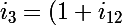^{\frac{3}{12}} - 1)
^{\frac{3}{12}} - 1 = (i\hat\ (4) / 4))
ou encore, pour remettre le "m" dans la course :
^{\frac{1}{m}} - 1 = (i\hat\ (m) / m))
ou encore :
 = (1+(i\hat\ (m) / m)^m)
En fait, l'argent suit une courbe exponentielle à tout moment. La valeur de l'argent A(t) est toujours de la forme = K \times e^{\lambda t}) . Choisissons t=0 au début de la période qui nous intéresse et l'année comme unité de temps, à t=0 on a :
. Choisissons t=0 au début de la période qui nous intéresse et l'année comme unité de temps, à t=0 on a :
 = K \times e^{0 \lambda} = K)
ce qui donne la valeur de K. Donc = A(0) \times e^{\lambda t})
au bout d'un an, on a :
 = A(0) \times e^{\lambda})
En comparant avec la formule faisant intervenir l'intérêt annuel réel :
 = A(0) * (1+i))
on constate que :
 = e^{\lambda})
ou

ou
})
Ceci permet de calculer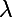 si on connaît i et vice-versa.
si on connaît i et vice-versa.
Si = A(0) \times e^{\lambda t}) , la dérivée de A(t) est alors :
, la dérivée de A(t) est alors :
 = A(t) * \lambda)
ce qui fait que ce que tu appelles est égal à :
est égal à :
}{A(t)} = \lambda)
Je rapprocherai ces formules de certaines de tiennes (pas toutes : je n'ai pas tout compris ce que tu as écrit, notamment la différence en A(t) et a(t) (qui portent pourtant le même nom !)) :
On voit alors que ce que tu appelles est ce que j'appelle
est ce que j'appelle 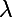
Toute autre considération dépasse ma compétence. Je constate en tous cas que tu maîtrises bien ton sujet et que tu as répondu toi-même à trois des quatre questions posées dans ton exercice :
1) 1 + i = [1 + (i^(m)/m)]^m
C'est la formule que tu m'as donnée ! Donc pour moi c'est VRAI
2) 1 + i = e^-;)
Cette formule est en contradiction avec ce que tu as dit plus haut : "1 + i = e^;)". Donc 2) est FAUX
3) > i
> i
Tu as écrit plus haut : ";) = ln(1 + i)" donc l'affirmation > i est équivalente à
> i est équivalente à
ln(1 + i)>i et on sait que ln(1+x) < x donc 3) est FAUX
4) i^(4) = 4(e^;) - 1)
Par contre, tu as dit et répété que l'expression (i^(m)/m) n'était pas mathématique : je suis donc obligé de la prendre comme un tout, et je ne sais donc pas ce que signifie i^(4) !!! Désolé, ça me dépasse !
Je suis déjà troublé par les définitions :
La notation "non mathématique" (d'après vous) (i^m)/m est extrêmement troublante. Si ce n'est pas mathématique, il ne faut pas l'employer dans des formules ! Si ça l'est, il doit bien y avoir une formule compréhensible par un mathématicien qui en donne une définition précise !
ElTopo a écrit:-De façon plus générale, le taux effetif d'intérêt i équivalent au taux nominal d'intérêt i^(m), correspondant à une situation pour laquelle l'intérêt est capitalisé m fois par période, est obtenu en considérant la valeur accumulée après un an lorsque 1$ est investi aux taux i et i^(m). Cette valeur accumulée est:
(1 + i) = (1 + (i^(m) / m))^m
Ici aussi, je suis perdu dans le texte, alors que je comprends la formule !
[INDENT]Pour moi, il n'y a qu'un seul taux annuel et toute cette discussion provient des inventions bizarroïdes de mots pour des choses qui ne correspondent à aucune réalité.
Si le taux réel annuel est i, le taux réel mensuel ne peut être autre chose que
A l'époque où nous avions des taux de 12% l'an (je veux dire que les banques affichaient "taux nominal = 12%), on s'apercevait que les calculs étaient parfaitement exacts à condition de prendre des taux mensuels de 1% exactement. Tous les guichetiers des banques soutenaient mordicus que le taux mensuel était le douzième du taux annuel. La raison est que l'utilisation d'une exponentielle dépasse largement les capacités intellectuelles du client moyen et que par suite les banques jugent inutile d'employer comme guichetier un type qui connaît les exponentielles vu que tout ce qu'il dirait ne pourrait être compris par l'homme de la rue ! Donc pour moi, 1% par mois, c'est
Appelons
Si je compare ta formule (1 + i) = (1 + (i^(m) / m))^m avec la mienne
ou encore, pour remettre le "m" dans la course :
ou encore :
En fait, l'argent suit une courbe exponentielle à tout moment. La valeur de l'argent A(t) est toujours de la forme
ce qui donne la valeur de K. Donc
au bout d'un an, on a :
En comparant avec la formule faisant intervenir l'intérêt annuel réel :
on constate que :
ou
ou
Ceci permet de calculer
Si
ce qui fait que ce que tu appelles
Je rapprocherai ces formules de certaines de tiennes (pas toutes : je n'ai pas tout compris ce que tu as écrit, notamment la différence en A(t) et a(t) (qui portent pourtant le même nom !)) :
ElTopo a écrit:En notant le taux effectif par i, nous avons 1 + i = e^;).
Conséquemment les équations:
i = e^;) - 1 et= ln(1 + i)
On voit alors que ce que tu appelles
Toute autre considération dépasse ma compétence. Je constate en tous cas que tu maîtrises bien ton sujet et que tu as répondu toi-même à trois des quatre questions posées dans ton exercice :
1) 1 + i = [1 + (i^(m)/m)]^m
C'est la formule que tu m'as donnée ! Donc pour moi c'est VRAI
2) 1 + i = e^-;)
Cette formule est en contradiction avec ce que tu as dit plus haut : "1 + i = e^;)". Donc 2) est FAUX
3)
Tu as écrit plus haut : ";) = ln(1 + i)" donc l'affirmation
ln(1 + i)>i et on sait que ln(1+x) < x donc 3) est FAUX
4) i^(4) = 4(e^;) - 1)
Par contre, tu as dit et répété que l'expression (i^(m)/m) n'était pas mathématique : je suis donc obligé de la prendre comme un tout, et je ne sais donc pas ce que signifie i^(4) !!! Désolé, ça me dépasse !
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
