Mesure image, théorème de transfert
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
par legeniedesalpages » 16 Déc 2007, 00:14
Bonsoir je bloque sur cet exercice:
Soient
)
un espace mesuré,
)
un espace mesurable et
une fonction
mesurable.
1) Montrer que, pour toute
)
,
[CENTER]
\ d\mu = \Bigint_F f\ d(\mu\circ h^{-1}).\qquad (1))
[/CENTER]
3) Déterminer
)
en fonction de
)
et de
.
Montrer que (1) perdûre sur cet espace.
4) Montrer que si
)
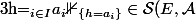, on a
[CENTER]
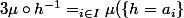\ \delta_{a_i})
[/CENTER]
Pour les notations:
=\{f: (F,\mathcal{B})\rightarrow ([0,+\infty],\mathcal{B}([0,+\infty]):\ f \mbox{ mesurable }\})
)
= { les fonctions simples définies sur
)
}
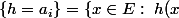=a_i\})
est la masse de Dirac en
Pour la 1, 2 et 3, pas de souci,
mais je sèche complètement sur la question 4.
Merci pour votre aide
par legeniedesalpages » 16 Déc 2007, 01:54
Bon je suppose que pour la 4),
 = ([0,+\infty],\mathcal{B}([0,+\infty]))
si
est définie ainsi.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 16 Déc 2007, 11:48
Salut "legeniedesalpages" :
c'est quoi
? ( c'est des ensembles ( des parties d'un ensemble ( je sais pas lequel, mais c'est ça l'idée ), ce sont les images inverses des singletons n'est ce pas ?! est ce que ces parties là sont disjoints ?! evidemment !! et voilà ! tu aboutis au resultat !
La mesure image, on l'a pas fait en cours ! :lol2:
Bonne courage !
par legeniedesalpages » 16 Déc 2007, 11:53
))
où
est une tribu sur l'ensemble d'arrivée F. C'est l'image réciproque.
par legeniedesalpages » 16 Déc 2007, 11:58
en fait dans 4) il demande de montrer que ces deux mesures coincident, vu qu'on est dans
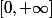
, je pense qu'il suffit de le montrer sur un générateur des boréliens de
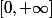
, mais je ne vois pas lequel et comment procéder.
Par contre l'ensemble des singletons n'est pas un pi système ou une classe monotone, je saisis pas vraiment ce que tu me proposes?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 16 Déc 2007, 12:03
Oui, voilà :
Tu prends un mesurable
:
 = \mu ( h^{-1} (A) ) = \mu ( h^{-1} (A) \bigcap ( \bigcup_{i \in I} \{ h = a_{i} \} )) = \mu ( \bigcup_{i \in I} ( h^{-1} (A) \bigcap \{ h = a_{i} \} )) = \displaystyle \sum_{ i \in I } \mu ( h^{-1} (A) \bigcap \{ h = a_{i} \} ) ... etc $)
C'est ça , n'est ce pas ?
par legeniedesalpages » 16 Déc 2007, 12:10
oui je suis d'accord, mais c'est après que ça se complique pour faire apparaitre cette satanée masse de Dirac. :cry:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 16 Déc 2007, 12:18
 \bigcap \{ h = a_{i} \} ) = \mu ( \{ h = a_{i} \} ) . \delta_{a_{i}}(A) $)
...
est aussi une mesure comme
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 16 Déc 2007, 12:20
tu discutes les cas ou la mesure de dirac est egale à
et dans quel cas elle est egale à
! n'est ce pas ?
par legeniedesalpages » 16 Déc 2007, 12:23
barbu23 a écrit: \bigcup \{ h = a_{i} \} ) = \mu ( \{ h = a_{i} \} ) . \delta_{a_{i}}(A) $)
...
est aussi une mesure comme
ok je vais suivre tes pistes
, enfin je suppose que tu veux dire
 \bigcap \{ h = a_{i} \} ) = \mu ( \{ h = a_{i} \} ) . \delta_{a_{i}}(A))
?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 16 Déc 2007, 12:28
oui, voilà ! :++:
par legeniedesalpages » 16 Déc 2007, 13:02
ok ça fonctionne nickel, merci Barbu tu m'as sauvé la vie :king2:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
