Mesure-image

[legeniedesalpages]

Bonsoir,

Soit une application mesurable, et soit un mesure sur .

Je cherche un exemple où est une mesure -finie et où la mesure image de par qu'on note n'est pas -finie.

Merci pour vos indications.

[legeniedesalpages]

:triste: :hein: :help:

[tize]

Bonjour,
de manière assez simple avec .
est mesurable, la mesure de Borel est -finie mais la mesure image ne l'est pas :

[BQss]

Bonjour,
de manière assez simple avec .
est mesurable, la mesure de Borel est -finie mais la mesure image ne l'est pas :

Salut Tize,
ta mesure est sigma finie en prenant comme suite


avec la mesure de lebesgue

et

[legeniedesalpages]

Bonjour,
de manière assez simple avec .
est mesurable, la mesure de Borel est -finie mais la mesure image ne l'est pas :

Mais ton égalité nous dit juste que n'est pas finie, je vois pas en quoi l'on doit déduire de cette égalité que n'est pas -finie.

[tize]

Exact BQss et Legenie
désolé d'avoir dit une bêtise :briques:
Que dites vous de remplacer par ?

[BQss]

sin(x) me semble bon, pour tout intervalle different du singleton inclu dans [-1;1], la mesure image est infinie... Donc on ne pourra pas construire la suite.

[BQss]

En fait, on se rend compte que toute fonction periodique bornée, p.partout non constante et continue, n'est pas par rapport a la mesure de Lebesgue. Bien vu Tize.

Pour affaiblir les hypothèses, on pourrait dire que toute fonction, continue par morceau de support , tel que avec A de mesure non nulle et B de mesure finie, est non sigma finie relativement a la mesure de Lebesgue.

[legeniedesalpages]

sin(x) me semble bon, pour tout intervalle different du singleton inclu dans [-1;1], la mesure image est infinie... Donc on ne pourra pas construire la suite.

je ne comprend pas, on prend donc la fonction mesurable , avec .

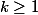
On veut montrer que n'est pas -finie, c'est à dire que pour toute suite croissante de parties de telle que , il existe tel que .

D'après ce que dit BQss, on utilise l'argument qu'à partir d'un certain rang ,
contient un intervalle ouvert, mais je ne vois pas pourquoi? :hein: