Recherche de fonction
35 messages
- Page 2 sur 2 - 1, 2
nuage a écrit:Salut,
une partie du problème vient de ce que beaucoup de fonctions vérifient les conditions demandées.
Dans le genre simple on peut prendre des fonctions puissances.
Par exemple :
avecpour avoir la 1° somme égale à 1
etpour avoir la 2° somme égale à 0.
Il faut de plus avoir r>0 et s>0, mais ça laisse encore pas mal de choix possibles.
Le tout sauf erreurs de calcul de ma part.
Ben je teste ca. je le sens bien. des que je sais je vous en informe.
Juste pour le plaisir:
il faut savoir que cette equation me permettra de traiter d'un processus microphysique qui a lieu au sommet des nuages. je trouverais plutot genial que ce soit "nuage" qui est finalement la solution.
Merci
Bonjour Thouron,
j'ai bien reçu ton message mais je ne comprends pas trop ce qui te gêne, Nuage a résolu le problème, non ?
on a :(r+2)=\gamma(s+1)(s+2)) avec
avec 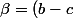^2) et
et 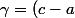^2) , tu choisis
, tu choisis  comme tu veux (presque au hasard) de manière à ce qu'il existe une racine positive de l'équation en s (il faut regarder le discriminant) et une fois que tu as r et s tu en déduit simplement k, non ?
comme tu veux (presque au hasard) de manière à ce qu'il existe une racine positive de l'équation en s (il faut regarder le discriminant) et une fois que tu as r et s tu en déduit simplement k, non ?
j'ai bien reçu ton message mais je ne comprends pas trop ce qui te gêne, Nuage a résolu le problème, non ?
on a :
tize a écrit:Bonjour Thouron,
j'ai bien reçu ton message mais je ne comprends pas trop ce qui te gêne, Nuage a résolu le problème, non ?
on a :avec
et
, tu choisis
comme tu veux (presque au hasard) de manière à ce qu'il existe une racine positive de l'équation en s (il faut regarder le discriminant) et une fois que tu as r et s tu en déduit simplement k, non ?
ben en fait je n'avais pas vu le probleme sous cet angle. Désolée. Je ragarde ca. Je te remercie encore et encore. Surtout pour ta rapidité.
Sincerement.
Salut,
je ne trouve pas tout à fait la même chose:
Tout d'abord, le facteur k peut être enlevé car la somme des intégrales est égale à 0...cela donne d'une part (avec IPP) :
^rdx=\frac{1}{(c-a)^r}\int_{a}^{c}x\(x-a\)^rdx) et
et ^rdx = \[x\times\frac{(x-a)^{r+1}}{r+1}\]_{a}^{c}-\int_{a}^{c}\frac{(x-a)^{r+1}}{r+1}dx=\frac{c(c-a)^{r+1}}{r+1}-\[\frac{(x-a)^{r+2}}{(r+1)(r+2)}\]_{a}^{c}=\frac{c(c-a)^{r+1}}{r+1}-\frac{(c-a)^{r+2}}{(r+1)(r+2)})
Donc :
^rdx=c\times\frac{c-a}{r+1}-\frac{(c-a)^2}{(r+1)(r+2)})
De "même", j'ai :
^sdx=c\times\frac{b-c}{s+1}+\frac{(b-c)^2}{(s+1)(s+2)})
On doit donc trouver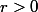 et
et 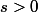 tels que :
tels que :
^2}{(r+1)(r+2)}+c\times\frac{b-c}{s+1}+\frac{(b-c)^2}{(s+1)(s+2)}=0)
On peut alors choisir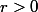 et ensuite résoudre l'équation en
et ensuite résoudre l'équation en  et prendre une solution positive (quitte à modifier
et prendre une solution positive (quitte à modifier  pour être sur d'avoir une solution positive pour
pour être sur d'avoir une solution positive pour  )
)
je ne trouve pas tout à fait la même chose:
Tout d'abord, le facteur k peut être enlevé car la somme des intégrales est égale à 0...cela donne d'une part (avec IPP) :
Donc :
De "même", j'ai :
On doit donc trouver
On peut alors choisir
tize a écrit:
On peut alors choisiret ensuite résoudre l'équation en
et prendre une solution positive (quitte à modifier
pour être sur d'avoir une solution positive pour
)
1)je suis aussi d'accord avec ta méthode de calcul. Je ragarderai demain mais j espere que nos deux calculs sont égaux, sinon probleme et va bien falloir que je trouve ou est l erreur ...
2) seulement le choix de r et s va dependre de a, b et c ce qui va, j en ai bien peur, vite me ramener vers une resolution numérique et non analytique.
....
Je le promets, je vais tout faire pour que cette solution marche
tize a écrit:
nuage a écrit:=1)
Bon il y avait plusieurs erreurs qui me permettent de comprendre:
et nuage avait trouver
d'ou:
Sauf que en fait:
d'ou:
Sauf contradiction de votre part je pars sur ces equations. Mais j'ai un doute sur une solution analytique evidente, c'est à dire trouver une valeur de r qui permettra d'avoir des solutions pour s et k toujours correctes.
thouron a écrit:ok nos deux solutions sont equivalentes.
reste plus qu'à chercher une solution simple.... et non numérique
Simple c'est pas sur...
Pour simplifier, j'ai choisi de prendre r=1 ce qui donne :
qui donne à son tour :
35 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
