Etude d'une fonction exponentielle complète

[arnaudrou]

Bonjour,

Qui peut me donner un coup de main pour mon dm qui est une étude de fonction exponentielle, la question 4)b) et 5b) le reste est ok

Partie A. Etude d'une fonction auxiliaire
(je pose ¤ = alpha )

Soit la fonction g définie sur R par g(x)= e^x + x +1.
1.Etudier les limites de g en +oo et en -oo,
--> en +oo = +oo et en -oo=-oo
2.Etudier le sens de variation de g sur R.
-->dérivé positive, croissant
3.a) Démontrer que l'équation g(x) = 0 admet, sur R, une solution unique ¤
--->corrolaire étendu des valeurs intermédiaires
b) Justifier l'encadrement — 1, 28 < ¤ < —1,27.
-->balayage
4.En déduire le signe de g(x) sur R.
---> négatif en dessus de et positive au dessus

Partie B. Etude de la fonction principale

Soit la fonction f définie sur R par f(x)= (xe^x)/(e^x+1)
C désigne sa courbe représentative dans un repère orthonormal (0 , i , j )

1.Déterminer la limite de f en -oo.. Interpréter géométriquement ce résultat.
2.a) Etudier la limite de f en +oo.
b)Démontrer que la droite D d'équation y = x est asymptote à C.
c)Etudier la position de C par rapport à D.
3.Vérifier que x appartenant à R, f'(x)=(e^xg(x))/(e^x+1)² et en déduire les variations de f sur R .
4.a) Montrer que f(¤) = ¤ +1.
--> pas de soucis jusque la
b) En déduire un encadrement de f(¤).
-->la je vois pas...
5.a) Déterminer une équation de la tangente T à C au point d'abscisse O.
--> pas de soucis on trouve 1/2x
b) Etudier la position relative de C par rapport à T.
--> la je n'arrive pas a étudier le signe de f(x)-1/2x = (xe^x-x)/(2(e^x+1))


Merci d'avance

[Fred_Sabonnères]

Tu as montré précédemment

Tu viens de montrer
tu en déduis
Tu conclus...

[arnaudrou]

on en conclut:

-0.28< ¤+1 < -0.27

?? ca donne pas d'encadrement de f(¤) :cry:

[Fred_Sabonnères]

Pour la dernière question, il s'agit d'étudier le signe de sur
Regarde le signe de x sur
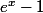
Regarde le signe de sur
Déduis en le signe du produit

[Fred_Sabonnères]

on en conclut:

-0.28< ¤+1 < -0.27

?? ca donne pas d'encadrement de f(¤)

si
et que tu montres
alors

[arnaudrou]

oui en faite ce qui me pose problème c'est d'étudier le signe de e^x-1 sur R je ne sais pas comment on fait...

[Fred_Sabonnères]

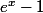
oui en faite ce qui me pose problème c'est d'étudier le signe de sur R je ne sais pas comment on fait...

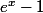
La fonction est strictement croissante sur R et s'annule en
Tu en déduis la suite

[arnaudrou]

on en déduit:

f(x)-1/2x < 0 sur ]-oo ; 0[ donc T au dessus de C
f(x)-1/2x > 0 sur ]0 ; +oo[ donc C au dessus de T

c'est bizare ca correspond pas au graphique !!

c'est bon??

[arnaudrou]

au faite il y aussi ce détail ou je ne vois pas ou ils veulent en venir dans la 1 de la partie B: "Interpréter géométriquement ce résultat." sachant que j'ai trouvé limf(x) = 0 en -oo

edit: tout simplement: " La droite d'équation y = 0 est asymptote à la courbe en - oo "

[arnaudrou]

Je n'arrive pas à prouver avec ce calcul:
(xe^x)/(e^x+1)-1/2x = (xe^x-x)/(2(e^x+1))

que C est au dessus de T


:mur: :mur:

[Fred_Sabonnères]

Rien ne vaut un bon vieux tableau



Donc C est toujours au dessus de T