Bonjour,
Je dois trouver les points invariants de la fonction f : z->(z+i)/(z-i)
J'ai donc trouvé que cela revenait à résoudre l'équation polynomiale complexe -z^2+z(1+i)+i=0
Mais c'est la première fois que je rencontre une équation complexe ayant un discriminant avec des imaginaires et je ne sais pas comment résoudre cette équation.
Merci d'avance pour vos réponses
Equations complexes
2 messages
- Page 1 sur 1
Bonjour,
Les solutions d'une équation de degré deux à coefficients complexes sont
sont 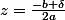 et
et 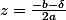 , où
, où  est une racine carrée du discriminant, c'est-à-dire qu'on a
est une racine carrée du discriminant, c'est-à-dire qu'on a 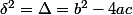 .
.
Le problème se ramène donc à la recherche des racines carrées d'un nombre complexe. On montre facilement que tout nombre complexe non nul possède deux racines carrées opposées en utilisant la forme exponentielle : si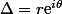 avec
avec 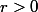 , alors ces racines carrées sont
, alors ces racines carrées sont 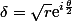 et
et  .
.
Les solutions d'une équation de degré deux à coefficients complexes
Le problème se ramène donc à la recherche des racines carrées d'un nombre complexe. On montre facilement que tout nombre complexe non nul possède deux racines carrées opposées en utilisant la forme exponentielle : si
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
