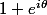Nombres complexes : équations dans C, argument et ensemble d
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
besten
- Membre Naturel
- Messages: 39
- Enregistré le: 29 Jan 2012, 18:52
-
 par besten » 31 Jan 2012, 09:43
par besten » 31 Jan 2012, 09:43
Bonjour,
J'aimerais résoudre ces exos mais je ne les comprends pas les deux premiers, et ne sais pas résoudre le troisième exo. Estce que vous pouvez me donner des éléments de réponse ?

-
euler21
- Membre Relatif
- Messages: 313
- Enregistré le: 26 Aoû 2009, 02:40
-
 par euler21 » 31 Jan 2012, 09:58
par euler21 » 31 Jan 2012, 09:58
Bonjour
pour le premier exercice, il faut utiliser "une formule célèbre" pour changer l'expression de
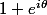
pour le deuxième, utilise la caractérisation d'un nombre complexe réel et d'un nombre complexe imaginaire pur (relation de z avec son conjugué)
-
besten
- Membre Naturel
- Messages: 39
- Enregistré le: 29 Jan 2012, 18:52
-
 par besten » 31 Jan 2012, 10:13
par besten » 31 Jan 2012, 10:13
euler21 a écrit: pour le premier exercice, il faut utiliser "une formule célèbre" pour changer l'expression de
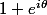
et ensuite, à quoi ça doit nous mener ?
euler21 a écrit:pour le deuxième, utilise la caractérisation d'un nombre complexe réel et d'un nombre complexe imaginaire pur (relation de z avec son conjugué)
je ne vois pas de quoi tu parles...
-
euler21
- Membre Relatif
- Messages: 313
- Enregistré le: 26 Aoû 2009, 02:40
-
 par euler21 » 31 Jan 2012, 10:24
par euler21 » 31 Jan 2012, 10:24
essaie d'écrire
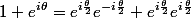
Pour la deuxième , Z complexe est réel si et seulement si
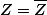
...
-
besten
- Membre Naturel
- Messages: 39
- Enregistré le: 29 Jan 2012, 18:52
-
 par besten » 31 Jan 2012, 16:06
par besten » 31 Jan 2012, 16:06
Je comprends pas...
Je vais essayer quand même.
Pour le 2.2 et 2.3 ?
Et pour l'exo 3 ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 31 Jan 2012, 16:42
par Dinozzo13 » 31 Jan 2012, 16:42
Salut !
Pour l'exercice III :
1°) Pose

,

et

les affixes respectives des points

,

et

.
Par suite :

.
2°) Fais de même, tu arriveras à

.
Désigne

le barycentre des points pondérés
,\(B,\frac{1}{2} \))
et continue :++:
-
besten
- Membre Naturel
- Messages: 39
- Enregistré le: 29 Jan 2012, 18:52
-
 par besten » 01 Fév 2012, 04:22
par besten » 01 Fév 2012, 04:22
Merci mais ce n'est que le début d'année donc la notion de barycentre m'est inconnue.
Je n'ai pas compris à quoi mener la transformation de z, 3 et 5 en lettre.
On ne m'a toujours pas expliqué les exos 1 et 2 de façon simple.
C'est possible de m'expliquer ?
-
mathelot
 par mathelot » 01 Fév 2012, 08:10
par mathelot » 01 Fév 2012, 08:10
Bonjour
exercice 1
est réel si et seulement si il est égal à son conjugué

par produit en croix
=1-(z-\bar{z}))
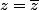

réel si et seulement si

réel
l'exercice 2 peut se traiter de même
exercice 3
équivaut

on écrit des modules de différences
|=|z-1|)
on en déduit que l'homographie applique la la médiatrice de A(1),B(-1) sur le cercle
centré en O, de rayon 1.
-
besten
- Membre Naturel
- Messages: 39
- Enregistré le: 29 Jan 2012, 18:52
-
 par besten » 01 Fév 2012, 19:20
par besten » 01 Fév 2012, 19:20
Merci mathelot !

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 01 Fév 2012, 21:01
par Sa Majesté » 01 Fév 2012, 21:01
mathelot a écrit:
réel si et seulement si

réel
Différent de 1 quand même
-
besten
- Membre Naturel
- Messages: 39
- Enregistré le: 29 Jan 2012, 18:52
-
 par besten » 04 Fév 2012, 03:27
par besten » 04 Fév 2012, 03:27
Merci pour toutes les infos mais je n'ai pas réussi à faire l'exercice 1.
Pour l'exercice 2, je n'ai pas compris le numéro 3, soit le module de |(1+z)/(1-z)|=1
Je ne sais pas comment faire l'exercice 3...
-
besten
- Membre Naturel
- Messages: 39
- Enregistré le: 29 Jan 2012, 18:52
-
 par besten » 14 Fév 2012, 22:37
par besten » 14 Fév 2012, 22:37
J'ai un autre petit problème qui n'est pas non plus un problème.
Je ne sais pas comment faire, pourriez-vous me donner des pistes pour résoudre ces questions ?

Je vous taperai les réponses des exercices précédent si cela vous intéresse.
-
mathelot
 par mathelot » 16 Fév 2012, 07:47
par mathelot » 16 Fév 2012, 07:47
Bonjour
pour la (1) , tous les carrés de distances et de normes , dans le plan complexe,
sont des produits que l'on développe par double distributivité
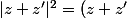(\overline{z}+\overline{z'}))
tu vas tomber sur l'égalité du parallélogramme
la somme des carrés des longueurs de diagonales est la somme des carrés des longueurs des côtés
pour la (2) , me^me technique
écris
=\overline{h(z)})
et utilise les propriétés de la conjugaison (morphisme de corps), compatible avec +,x,/
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités