Espace de sobolev
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
smooth5185
- Membre Naturel
- Messages: 21
- Enregistré le: 21 Oct 2007, 12:04
-
 par smooth5185 » 04 Nov 2007, 19:37
par smooth5185 » 04 Nov 2007, 19:37
Bonjour,
voila j'ai un probleme avec un exercice,
une aide serait precieuse, merci :)
Soit f appartenant a L1,loc(R) faiblement derivable tq f' appartienne a L2(R).
1)mq la forme lineaire (phi)f'(g)=-int(f(x)*d/dx(g(x))dx pour g appartenant a Cinf,c(R) s'etend en une forme lineaire continue sur L2(R).
2)mq f appartient a H1(R)
-
smooth5185
- Membre Naturel
- Messages: 21
- Enregistré le: 21 Oct 2007, 12:04
-
 par smooth5185 » 05 Nov 2007, 12:27
par smooth5185 » 05 Nov 2007, 12:27
mais le plus important resta la question 2) puisqu'oin pourra ensuite generalier pour Hn(R)
-
smooth5185
- Membre Naturel
- Messages: 21
- Enregistré le: 21 Oct 2007, 12:04
-
 par smooth5185 » 05 Nov 2007, 20:32
par smooth5185 » 05 Nov 2007, 20:32
je crois que pour 1) il faut :
integré par parties pour faire apparaitre f' et utiliser Cauchy-Schwarz pour faire sortir la norme 2 de g.
mais apres comment en deduire la continuité??
Merci.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 05 Nov 2007, 20:39
par yos » 05 Nov 2007, 20:39
Bonsoir.
C'est un peu loin pour moi les espaces de Sobolev, mais essayons.
Pour la 1, c'est ce que tu dis et la continuité provient peut-être d'un argument de densité ?
Pour la 2, peux-tu me donner la définition de
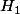
?
-
smooth5185
- Membre Naturel
- Messages: 21
- Enregistré le: 21 Oct 2007, 12:04
-
 par smooth5185 » 05 Nov 2007, 21:23
par smooth5185 » 05 Nov 2007, 21:23
pour la 1) on sait que Cinf,c(R) est dense dans L2(R) mais pour en conclure la continuité je ne vois pas.
pour la 2) H1={f appartenant a L2(R) tel que l'integrale de( (la transformation de fourier de f)^2 * (1+k)^2 )dk Merci bien .
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 05 Nov 2007, 23:51
par yos » 05 Nov 2007, 23:51
smooth5185 a écrit:mais pour en conclure la continuité je ne vois pas.
hum... je pensais à Hahn-Banach mais ça va pas aller car il postule l'existence et l'unicité d'un prolongement continu. Oublie.
Ca vaut mieux directement avec la formule
=\int f'g)
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
