Calcul d'une dérivée simple

par **loloc** » 21 Sep 2005, 08:13

Bonjour ,

voila le prof ns a demandé de trouver la dérivé de ln ( | u(x) | ) , les valeurs absolues st très importantes :)

la dérivée de ln ( u(x) ) c'est u' / u mais avec les valeurs absolues ??

Merci bcp d'avance , c'est assez urgent :)

par **Nicolas_75** » 21 Sep 2005, 08:49

Tu connais l'expression de u(x) ou pas ?

par **Anonyme** » 21 Sep 2005, 09:06

non u est dérivable , c'est tout ce que l'on sait :)

par **Nicolas_75** » 21 Sep 2005, 09:09

Sur tous les intervalles ouverts où u ne s'annule pas,

est dérivable, et sa dérivée est

Sauf erreur.

Nicolas

par **Anonyme** » 21 Sep 2005, 12:46

tu es sur ? Ce serait dc la meme chose que s'il n'y avait pas de valeur absolue :s ??

par **Ismail** » 21 Sep 2005, 13:16

Salut
je crois qu'il faut distinguer 2 cas ,lorsque u(x)>0 on a f(x)=ln(u(x))
et lorsque u(x)<0 alors f(x)=ln(-u(x))
et on trouve une derivée pour chaque cas
ou bien encore utiliser la formule |x|=V(x)^2

par **Nicolas_75** » 21 Sep 2005, 13:37

Ismail,

(1) On ne peut pas utiliser

car on ne connaît pas le signe de

(2) Tu as raison, il faut distinguer les cas. Mais on obtient le même résultat.
Sur un intervalle où u(x) est >0,

Sur un intervalle où u(x) est <0,

Sauf erreur, cela démontre mon résultat d'un message précédent.

Nicolas

par **Ismail** » 21 Sep 2005, 22:49

je voulais plutot ecrire

par **Adsederq** » 22 Sep 2005, 03:08

Ca serait pas plustot que dans les réel ln(x) implique pour que ln est une solution que x soit strictement positif de la les valeurs absolut?
ln(-2) par exemple, sur une calculatrice ca dit : error 2...donc que imposible dans les Réels...
ln|x| a une solution car x est positif, c'est tout, ln est une focntion strictement positive, alors quand ton prof dit que ln(|u(x)|) , les valeurs absolut sont importante, Il a bien raison!!

par **Nicolas_75** » 22 Sep 2005, 07:37

Reprenons dans l'ordre

"Ca serait pas plutôt que dans les réels ln(x) implique pour que ln ait une solution que x soit strictement positif de là les valeurs absolues?"
Non. Pour que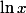

soit définie (et non pas qu'elle ait une solution, ce qui ne veut rien dire), il faut que x soit strictement positif

"ln|x| a une solution car x est positif, c'est tout"
Non.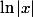

est défini car x non nul.

" ln est une fonction strictement positive"
Non. ln peut s'annuler (en 1) ou prendre des valeurs strictement négatives (sur ]0;1[)

par **Adsederq** » 23 Sep 2005, 21:20

Merci Nicola ;)

Et puis, pour le question de défini, je te remercie, je vais m'en rappeller que défini est le mot et non pas solution.. -(...
Et au sujet de ln négatif, a part dans les complexes, je vois pas comment, pcq sur ma calculette, des que ln est <1 ca dit : error 2 (ca dit ca aussi quand on divise par 0).
:zen:

par **phenomene** » 23 Sep 2005, 21:56

Ne pas confondre "

est strictement positif" avec "

est défini pour

strictement positif".

par **Adsederq** » 26 Sep 2005, 16:59

La différence c'est quoi en clairement ? Je sais qu'il y en a une mais expliquer de façon précise qu'Es-ce que c'est...

Calcul d'une dérivée simple

Calcul d'une dérivée simple

Qui est en ligne