Calcul d'une intégrale apparemment simple

[Jacky22]

Bonjour,

J'éprouve des difficultés pour calculer cette intégrale :
I=

Une première idée a été de poser une IPP :
u=ln(x) v'=1/1+x^2 --> u'=1/x v=arctan(x)

Ce qui mène à
I=

Ensuite, impossible d'arriver à un résultat!

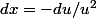
En posant J= et en faisant un changement de variable u=1/x (), j'arrive à

J=-

Je suppose qu'il faut utiliser le fait que sur R+ on a


Mais je sais pas si c'est la bonne voie et je n'y arrive vraiment pas.

Merci d'avance pour vos idées.

[Jacky22]

Resalut,

En fait, j'ai fait une erreur au niveau de mon dernier changement de variable :
J=
(Il n'y a pas de - car les bornes de l'intégrale sont inversées!)

Du coup, on a 2J=
ce qui implique

J=

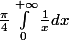
Et

I=

Mais ça parait pas défini ce truc? Non?

[Djmaxgamer]

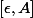
L'IPP est valable pour l'intégration sur un segment. Refait les même calculs sur puis fait tendre vers 0 et vers

EDIT : plutôt sur

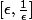
[Jacky22]

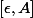
L'IPP est valable pour l'intégration sur un segment. Refait les même calculs sur puis fait tendre vers 0 et vers

EDIT : plutôt sur

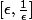
Merci même si ça ne me parait pas très clair ce que tu suggères. Néanmoins, après réflexion, on a

en utilisant la formule arctan(x)+arctan(1/x)=pi/2

Du coup, I=0 et c'est dans la poche.

Merci !

[chan79]

Bonjour,

J'éprouve des difficultés pour calculer cette intégrale :
I=

Une première idée a été de poser une IPP :
u=ln(x) v'=1/1+x^2 --> u'=1/x v=arctan(x)

Ce qui mène à
I=

Ensuite, impossible d'arriver à un résultat!

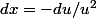
En posant J= et en faisant un changement de variable u=1/x (), j'arrive à

J=-

Je suppose qu'il faut utiliser le fait que sur R+ on a


Mais je sais pas si c'est la bonne voie et je n'y arrive vraiment pas.

Merci d'avance pour vos idées.

Une idée
Calcule l'intégrale pour x variant de 1 à a (avec a>1) et fais le changement de variable x=1/u

[Jacky22]

Merci chan79, effectivement c'est beaucoup plus simple en posant directement u=1/x car on arrive à
I=-I et donc I=0!