Bonjour,
samedi 22 septembre, pour bien commencer la journée, je vous propose cet exercice:
Une statue de hauteur s est plaçée sur un piédestal de hauteur p. A quelle distance doit se placer un observateur (dont la taille est supposée négligeable) pour voir la statue sous un angle maximal ? :briques:
indication: Arctan
Cordialement,
Voir une statue sous son meilleur angle
4 messages
- Page 1 sur 1
Comment fais-tu cette construction ?
Le signe de la fonction)
est celui du trinôme:
 \right))
Le meilleur angle d'observation de la statue est obtenu à une distance
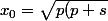})
On doit donc préprogrammer cette fonction sur sa calculatrice avant d'aller
au musée ou se promener dans un parc.. :zen:
Le meilleur angle est donc:
 - \, \frac{\pi}{2})
cordialement,
Le signe de la fonction
est celui du trinôme:
Le meilleur angle d'observation de la statue est obtenu à une distance
On doit donc préprogrammer cette fonction sur sa calculatrice avant d'aller
au musée ou se promener dans un parc.. :zen:
Le meilleur angle est donc:
cordialement,
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
