Monotonie d'une suite

par **ludo74** » 19 Sep 2007, 12:57

Bonjour à tous j'ai un petit problème sur la monotonie d'une suite pourriez vous me donner un petit coup de main:

voici la suite

et pour tout

je ne vois pas bien comment étudier la monotonie je sais grace a ma calculatrice que la suite ted vers 2 et qu'elle est décroissante mais je ne sais pas comment le prouver

par **fonfon** » 19 Sep 2007, 13:09

salut,

en calculant U(n+1)-Un et en utilisant l'expression conjuguée ça devrait aller

par **yos** » 19 Sep 2007, 13:13

Bonjour.
On peut dire que

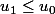
et

est croissante. Donc u est décroissante.

par **ludo74** » 19 Sep 2007, 13:36

fofon je voulais faire ta méthode mais étant donné que je n'ai pas la formule explicite comment puis je calculer Un???

par **ludo74** » 19 Sep 2007, 14:01

vraiment cest très important pour moi de comprendre j'ai un ds dans peu de temps si quelqu'un pouvait m'aider j'en serais vraiment ravi

par **fonfon** » 19 Sep 2007, 14:18

il vaut mieux que tu utilises ce que Yos a donné c'est plus rapide ,moi je t'avais donné ça car j'avais jeter un coup d'oeuil rapide et en plus ça donne des calculs plus longs

par **ludo74** » 19 Sep 2007, 14:27

daccord mais dans ce cas je dis que Uo > U1 et que racine de x+2 croissant mais après sa ne me prouve pas que Un décroissante c'est pour cette raison que je ne comprends pas le raisonnement

par **ludo74** » 19 Sep 2007, 21:12

y'aurait il quelqu'un pour m'expliquer le raisonnement

par **yos** » 20 Sep 2007, 11:28

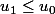
et tu appliques la fonction croissante $:x$ \mapsto \sqrt{2+x}"/>.
Ca te donne

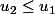
puis en recommençant

, etc.
Ecris la preuve par récurrence.

Monotonie d'une suite

monotonie d'une suite

Qui est en ligne