Suite, monotonie

[Piickles]

Bonjours, voici le p'tit exercice:

Soit la suite w, définie pour tout entier naturel n par :
Démontrer que pour tout n 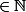, on a 1. Conclure sur la monotonie de W.
----

=

Seulement après j'bloque pour diminuer tout ça... :help:

Merci d'avance.

[Piickles]

à peine écrit que j'arrive à avancer enfaite un peu :

x

[uztop]

Bonjour,

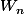
quelle est la définition de ; elle semble changer selon le lignes.
Est ce que c'est (donc avec (n+1) en puissance) ?

[Piickles]

il n'y a pas de puissance au numérateur.


[Oupz tu as raisons j'me suis tromper au deuxième message ce n'est pas
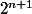
mais désolé. Avec (n+1) pour être plus précise.]

[uztop]

euh désolé mais ça ne veut rien dire

[Piickles]

Ben je remplace dans l'équation de départ n par n+1 pour répondre à l'énoncé de l'exercice qui veut qu'on trouve que est inférieur à 1
donc à la place de je mets

[uztop]

oui je comprends bien mais la notation ou n'a pas de sens en maths.
A mon avis, le (n+1) est en exposant (pour faire une puissance).

[Piickles]

Ah baaah oui tu dois avoir raisons Merci
Plus qu'à refaire avec n+1 en puissance alors

ce qui donne x

[uztop]

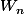
est ce que la définition de est
ou ?

[Piickles]

2_n + 1 sur

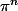
[uztop]

ok, dans le produit que tu as calculé, les termes en se simplifient, et il te reste donc
Pour montrer le résultat qu'on te demande, tu dois donc montrer que (ou autre chose qui est plut petit que
Pour celà, il faut essayer de transformer le numérateur pour y reconnaitre le dénominateur, ou quelque chose qui y ressemble assez.

[Piickles]

est-ce que x est égale à ? j'viens de voir que dans mon cours mon professeur l'a fait pour un autre exemple enfin je trouve qd même ça étrange mmm.. mais si on peut je pourrai simplifié et arriver à inférieur à 1
Donc 1
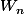
car positif et la suite W est strictement décroissante.. donc monotone

[uztop]

oui en effet ; c'est d'ailleurs ça qu'il faut utiliser pour résoudre ton exercice (il faut mettre 2 en facteur au numérateur)