Exercice analyse
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 22 Juil 2007, 18:06
par J-R » 22 Juil 2007, 18:06
bonsoir,
un exercice me pose problème:
Soit a un réel et f une application de R vers R dérivable en a telle que : f(a)=a et
=\frac{1}{4})
Justifier qu'il existe un intervalle I contenant a vérifiant:
si

alors
-a}{x-a}-\frac{1}{4}|\le \frac{1}{2})
merci
:++:
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 22 Juil 2007, 18:10
par anima » 22 Juil 2007, 18:10
J-R a écrit:bonsoir,
un exercice me pose problème:
Soit a un réel et f une application de R vers R dérivable en a telle que : f(a)=a et
=\frac{1}{4})
Justifier qu'il existe un intervalle I contenant a vérifiant:
si

alors
-a}{x-a}-\frac{1}{4}|\le \frac{1}{2})
merci
:++:
Qu'est-ce que
-f(x_0)}{x-x_0})
évoque pour toi?
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 22 Juil 2007, 18:13
par J-R » 22 Juil 2007, 18:13
bonsoir,
mais oui je sais que c'est le taux d'accroissement mais ce n'est pas égale à f'(a) car x ne tend pas forcément vers a ?
pour moi ca le membre de gauche n'est pas égale à 0.... :hein:
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 22 Juil 2007, 18:17
par anima » 22 Juil 2007, 18:17
J-R a écrit:bonsoir,
mais oui je sais que c'est le taux d'accroissement mais ce n'est pas égale à f'(a) car x ne tend pas forcément vers a ?
pour moi ca le membre de gauche n'est pas égale à 0.... :hein:
Ta fonction est dérivable, continue, et donc la dérivée est continue, non? Alors, que peux tu dire si:
- Tu as 0 pour x=a
- Pour le reste, tu as le taux de variation d'une variation ayant une dérivée continue sur un intervalle devant etre compris entre [-1/2;+1/2] pour satisfaire l'inéquation...
Alors?
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 22 Juil 2007, 18:21
par J-R » 22 Juil 2007, 18:21
mais le cas où x=a n'existe pas ?
une dérivée continue a quoi ca peut servir ?
quelle est la piste que vous voulez me donner car je ne sais pas où je vais là ....
merci
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 22 Juil 2007, 18:28
par anima » 22 Juil 2007, 18:28
J-R a écrit:mais le cas où x=a n'existe pas ?
a existe; on te dit f: x->f(x) R->R avec f(a)=a. C'est une supposition de l'énoncé.
une dérivée continue a quoi ca peut servir ?
Que peux-tu dire d'une fonction continue? Qu'elle peut se tracer d'un trait de crayon, et donc qu'elle ne passe pas d'une valeur a une autre (par exemple, de 1 vers 2 comme le fait la fonction qui a x associe la partie entiere de x.)
quelle est la piste que vous voulez me donner car je ne sais pas où je vais là ....
Je ne te donne pas une piste, j'essaye de réfléchir avec toi. Mais si j'étais toi, je justifierai en supposant que la fonction est dérivable (donc continue) sur R, et que sa dérivée est aussi continue sur R.
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 22 Juil 2007, 18:36
par J-R » 22 Juil 2007, 18:36
non mais je voulais dire que dans le rapport f(x)-a/(x-a) x doit etre différent de a ?
mais a quoi servira de montrer que f est dérivable sur R ?
je ne sais pas quoi réfléchir.... :hein:
je vais manger a+
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 22 Juil 2007, 18:39
par J-R » 22 Juil 2007, 18:39
et peut on supposer que (f(x)-a)/(x-a) = f'(a) si oui pourquoi car x ne tend pas forcément vers a (donc ce n'est pas forcément un taux d'accroissement ) ai-je raison ?
merci
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 22 Juil 2007, 19:01
par J-R » 22 Juil 2007, 19:01
s'il vous plait .....
merci :we:
-
cesar
- Membre Rationnel
- Messages: 841
- Enregistré le: 05 Juin 2005, 07:12
-
 par cesar » 22 Juil 2007, 19:54
par cesar » 22 Juil 2007, 19:54
J-R a écrit:non mais je voulais dire que dans le rapport f(x)-a/(x-a) x doit etre différent de a ?
anima t'a pourtant tout donné ou presque...
la limite de f(x)-a/(x-a)= f'(a)=1/4 lorsque x tend vers a...
donc f(x)-a/(x-a) -1/4 tend vers ? sur au moins un voisinage proche de a (un intervalle)...
si je vais plus loin, je te dis tout...et c'est plus du jeu...
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 23 Juil 2007, 11:32
par J-R » 23 Juil 2007, 11:32
Si considère x au voisinage de a alos on a bien un taux d'accoissement donc le membre de gauche tend vers 0 qui est inférieur à 1/2.....
mais cela ne prouve pas l'existence d'un intervalle ?
merci :)
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 23 Juil 2007, 12:48
par J-R » 23 Juil 2007, 12:48
s'il vous plait.....
merci :)
-
Ledescat
- Membre Naturel
- Messages: 98
- Enregistré le: 08 Juil 2007, 15:13
-
 par Ledescat » 23 Juil 2007, 13:36
par Ledescat » 23 Juil 2007, 13:36
Bonjour.
Le fait que f'(a)=1/4 signifie:
-f(a)}{x-a}=\fr{1}{4})
(1)
Et le fait que (c'est un cas général):
=\beta)
signifie:

[pour tout epsilon>0, il existe eta>0]
Tel que si

alors
-\beta| \leq \epsilon)
Ici, tu traduis (1) par ce que je viens de te dire.

tq si

alors
-f(a)}{x-a}-\fr{1}{4}|\leq \epsilon)
Comme ça marche pour
tout epsilon>0, tu peux prendre epsilon=1/2
Et ça devient:
Pour

,il existe
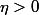
tel que si

, alors
-f(a)}{x-a}-\fr{1}{4}|\leq \fr{1}{2})
Et ton intervalle cherché est

(tu sais simplement qu'il existe)
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 23 Juil 2007, 13:52
par J-R » 23 Juil 2007, 13:52
ok c'est j'ai tout compris.
je vous remercie
en fait c'est une application directe d'une limite finie en un point (je verrais en terminale n'est ce pas ?)
a+ :++:
-
Ledescat
- Membre Naturel
- Messages: 98
- Enregistré le: 08 Juil 2007, 15:13
-
 par Ledescat » 23 Juil 2007, 13:53
par Ledescat » 23 Juil 2007, 13:53
J-R a écrit:
en fait c'est une application directe d'une limite finie en un point (je verrais en terminale n'est ce pas ?)
Exactement :we: .
Mais on revient très rarement (voire jamais) aux définitions fondamentales des limites en TS.
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 24 Juil 2007, 11:22
par theluckyluke » 24 Juil 2007, 11:22
Ta fonction est dérivable, continue, et donc la dérivée est continue, non?
n'existe il pas des fonctions dérivables qui admettent des dérivées non continues?
-
Ledescat
- Membre Naturel
- Messages: 98
- Enregistré le: 08 Juil 2007, 15:13
-
 par Ledescat » 24 Juil 2007, 11:35
par Ledescat » 24 Juil 2007, 11:35
En fait je n'arrive pas à en trouver. Car si la dérivée n'est pas continue en a, cela signifie que la pente à gauche et à droite en a sont différentes, donc que f n'était pas dérivable en a.
Quelqu'un pour la réponse ?
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 24 Juil 2007, 11:59
par anima » 24 Juil 2007, 11:59
Ledescat a écrit:En fait je n'arrive pas à en trouver. Car si la dérivée n'est pas continue en a, cela signifie que la pente à gauche et à droite en a sont différentes, donc que f n'était pas dérivable en a.
Quelqu'un pour la réponse ?

. continue. dérivable pour tout R sauf x=0, mais dérivable a gauche et a droite en ce point.
-
Ledescat
- Membre Naturel
- Messages: 98
- Enregistré le: 08 Juil 2007, 15:13
-
 par Ledescat » 24 Juil 2007, 12:40
par Ledescat » 24 Juil 2007, 12:40
anima a écrit:
. continue. dérivable pour tout R sauf x=0, mais
dérivable a gauche et a droite en ce point.
J'en doute.
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 24 Juil 2007, 12:43
par anima » 24 Juil 2007, 12:43
Ledescat a écrit:J'en doute.
Ah oui pardon, juste....J'ai dit une connerie.
Pour une fonction dérivable a gauche et a droite mais pas totalement, il faudrait prendre une fonction double, sur 2 intervalles.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités