Terminale S Dérivation

par **tonton-gaston** » 20 Mai 2007, 11:35

Bonjour a tous !

Je rame dans un exercice de maths qui a l'air tout con mais je bloque ...

Ex:

On pose pour n=0, n=1 et n=2, et pour tout x de ]-1;+infini[ :

fn(x) =

On note Cn la courbe représentant fn dans un repère orthonormal.

1. Expliquer pourquoi toutes les courbes Cn passent par le point de coordonnées (0;-1). On note A ce point.

2. Vérifiez que pour n=0, n=1 et n=2 :

f'n(x) = (n)/(1+x)^n+1
puis déduire la valeur de f'n(0)

MERCI d'y jetter un coup d'oeil ...

par **sue** » 20 Mai 2007, 11:55

Bonjour,

1)

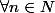
(puisque

)

2) pour n=0 c évident , pour n=1,2 tu utilise une formule du cours (1/u)'.

par **tonton-gaston** » 20 Mai 2007, 13:16

mince je n'ai pas tout compris la :S :S:S

par **sue** » 20 Mai 2007, 13:25

qu'est-ce que tu ne comprend pas ?

par **tonton-gaston** » 20 Mai 2007, 13:42

déja ton raisonnement pour la question 1. Je ne doute pas qu'il soit bon mais je ne comprends pas vraiment comment fait-on ... Excuse moi :S

par **sue** » 20 Mai 2007, 14:00

OK,

la question est d'expliquer pourquoi tous les courbes Cn passe par A(0,-1) .
si on remplace x par 0 (l'abscisse de A) on a

aprés tu sais que pour tout n de N on a

, donc même si n change on aura toujours

, autrement dit

(l'ordonnée de A) est indépendant de n .
donc toutes les courbe Cn passe par le point A(0,-1) .

ok ?

par **tonton-gaston** » 20 Mai 2007, 14:03

OK pour le moment je te suis la ca va !

par **guigui777** » 20 Mai 2007, 14:06

regarde le pont de coordonnée 0,-1 c'est à dire que si x=0, y=-1 ok?
tes fonctions sont définies pour n=0,n=1, n=2
en O t'a tout simplement f0=-1 donc une droite.... Y=-1 quelque soit x.... donc ca marche bien pour ton point
Pour n =1 tu as:
f1(x) = -1/(1+x) lorsque x=0 tu retrouve bien y=-1
et enfin n=2 tu as: f2(x) = -1/(1+x)².... lorsque x=0 t'a encore y = -1... donc tes trois courbes passent par -1 en 0.... tu fais une récurrence pour montrer que c'est vrai qlqsoit n...

par **sue** » 20 Mai 2007, 14:13

euh suffit pas de remarquer que

pour tout n de N ?
je crois pas qu'on a besoin d'une reccurence pour le montrer mais bon...

par **tonton-gaston** » 20 Mai 2007, 14:17

euh pour la question 2 je dois juste remplacer ou bien .... ?

par **sue** » 20 Mai 2007, 14:21

on te demande de vérifier pour n=0,1,2 , donc suffit de remplacer et de voir à chaque fois si ça colle avec la forme donnée .

par **tonton-gaston** » 20 Mai 2007, 14:29

ah ok effectivement ...
mais alors comment on connait la valeur de f'n(0) ?

Merci beaucoup de vos aides respéctives.

mais par exemple, pour la dernière question, il s'agit de tracer la tangete en A de chacune des courbes Co, C1 et C2

Comment je devrais faire pour trouver les coordonnées de la tangente ?

par **guigui777** » 20 Mai 2007, 14:32

sue a écrit:euh suffit pas de remarquer que pour tout n de N ?
je crois pas qu'on a besoin d'une reccurence pour le montrer mais bon...

ben disons que comme dirait mon prof de math ca fait plus mieux!

par **guigui777** » 20 Mai 2007, 14:37

tonton-gaston a écrit:ah ok effectivement ...
mais alors comment on connait la valeur de f'n(0) ?

Merci beaucoup de vos aides respéctives.

mais par exemple, pour la dernière question, il s'agit de tracer la tangete en A de chacune des courbes Co, C1 et C2

Comment je devrais faire pour trouver les coordonnées de la tangente ?

jpense que tu veux dire l'équation de la tangente... calcul ta dérivée c le coeff directeur de ta tangente en se point. donc comme c'est le coeff directeur, tu prends M(x,y) un^point qui se balade sur ta droite, tu cherches ensuite f' en O, et tu as f'(0)= (y-f(O))/(x-0)... tu en déduit y= f'(O)*x -f(O) et tu appliques cette formule pour tes trois courbes!!

par **tonton-gaston** » 20 Mai 2007, 14:43

Wow :hein: :hein: :hein:

par **guigui777** » 20 Mai 2007, 14:50

tonton-gaston a écrit:Wow :hein: :hein: :hein:

j'ai ptet pas été assez clair! ... dsl, donc tu cherches bien l'équation e la tangente?

par **tonton-gaston** » 20 Mai 2007, 14:54

ben en fait ouais je dois tracer la tangente a ces courbes SANS tracer ces courbes ....

donc oui je cherche bien l'équation de la tangente mais la c'est pas très concret pour moi excuse moi :S

par **guigui777** » 20 Mai 2007, 14:58

tonton-gaston a écrit:ben en fait ouais je dois tracer la tangente a ces courbes SANS tracer ces courbes ....

donc oui je cherche bien l'équation de la tangente mais la c'est pas très concret pour moi excuse moi :S

ben une tangente c'est ni plus ni moins qu'une droite.... t'es d'accord, donc tu cherche l'équation d'une droite en gros.... un truc de la forme ax+b... non?
le a est facile a déterminer car tu c'est que : la valeur de la dérivée en un point c'est le coeff directeur de ta tangente en CE point... c'est à dire la valeur de a en O.... tu vois le truc?

par **tonton-gaston** » 20 Mai 2007, 15:02

euh non en fait je vois pas le truc ( et non ! je ne le fais pas exprès ! c'est ca qui est inquiétant ... )

par **guigui777** » 20 Mai 2007, 15:08

tonton-gaston a écrit:euh non en fait je vois pas le truc ( et non ! je ne le fais pas exprès ! c'est ca qui est inquiétant ... )

euh déjà sais tu que le coeff directeur de la tangente en un point c la dérivée en ce point... ca c'est juste ton cours qui te le dis.. maintenant si tu ne le connais pas jpourrais pas bcp t'aider.

Terminale S Dérivation

Terminale S Dérivation

Qui est en ligne