Bonjour ,
Il s’agit de prouver que lim (u_n^3)/n^2= 9/4.
(u_n) étant la suite définie par :
u_0>0
u_(n+1)= u_(n) +( 1/ sqrt( u_n) )
J’ai essayé de considérer la fonction
f(x)= x+ 1/ sqrt(x) mais cela ne m’a pas fait avancer .
Merci pour votre guidance.
Limite d’une suite
11 messages
- Page 1 sur 1
Re: Limite d’une suite
Il n' y as d'équivalence, je suis partie de votre écrit (u_n^3)/n^2= 9/4 que j'ai écrit en Latex et j'ai fait les étapes décrites dans mon poste.
rappel :
je vous redonne le calcul.
^2 n^2 \quad \Rightarrow \quad u_n^3= (\dfrac{3n}{2} )^2 \quad \Rightarrow \quad u_n= (\dfrac{3n}{2} )^{\dfrac23)
rappel :
je vous redonne le calcul.
Re: Limite d’une suite
Pardon, mais je crois que vous n’avez pas repéré le symbole de limite : lim dans mon énoncé.
Re: Limite d’une suite
exacte,je n'ai pas mis le symbole limite, je pensais que vous sauriez le faire vous même. En fait je ne vous ai pas fait l'exercice,je vous ai juste donné une information qui pourrait vous aider.
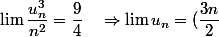^{\dfrac23})
Re: Limite d’une suite
êtes vous sur de votre énoncé? notamment :
u_0>0
u_(n+1)= u_(n) +( 1/ sqrt( u_n) )
u_0>0
u_(n+1)= u_(n) +( 1/ sqrt( u_n) )
Re: Limite d’une suite
Bonjour,
Je ne vois pas ce que l'énoncé aurait de douteux, et en passant l'écriture^{2/3}) ne fait pas sens. Ce qui fait sens, c'est de dire qu'il y a à montrer que
ne fait pas sens. Ce qui fait sens, c'est de dire qu'il y a à montrer que  est équivalent à
est équivalent à ^{2/3}) quand
quand 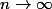 .
.
On peut remarquer que le relation de récurrence peut être récrite comme . Cela fait penser à l'équadiff
. Cela fait penser à l'équadiff  , qui se résout facilement puisqu'elle est à variables séparables. Après, ce rapprochement n'est pas évident à exploiter ....
, qui se résout facilement puisqu'elle est à variables séparables. Après, ce rapprochement n'est pas évident à exploiter ....
Je ne vois pas ce que l'énoncé aurait de douteux, et en passant l'écriture
On peut remarquer que le relation de récurrence peut être récrite comme
Re: Limite d’une suite
Sara1999 a écrit:Bonjour ,
Il s’agit de prouver que lim (u_n^3)/n^2= 9/4.
(u_n) étant la suite définie par :
u_0>0
u_(n+1)= u_(n) +( 1/ sqrt( u_n) )
J’ai essayé de considérer la fonction
f(x)= x+ 1/ sqrt(x) mais cela ne m’a pas fait avancer .
Merci pour votre guidance.
J'aurais plutôt tendance à exploiter la fonction pour qu'on arrive à nos fins. Puisque l'intervalle
C'est sûrement moins efficace que ce que Gabuzomeu suggère mais c'est peut-être plus classique comme démarche.
Re: Limite d’une suite
Merci GaBuZoMeu et ComeDuRondeau.
J’ai pu arriver au résultat grâce à votre indication.
Alpha est 3/2 et la limite de u_(n+1) ^3/2 -u_(n)^3/2 est égale à 3/2 . Seulement j’ai utilisé des encadrements faisant intervenir l’inégalité de Bernoulli au lieu du DL.
Maintenant je serais curieuse de connaitre une méthode non classique. Cela pourrait élargir mon savoir. Merci d’avance.
J’ai pu arriver au résultat grâce à votre indication.
Alpha est 3/2 et la limite de u_(n+1) ^3/2 -u_(n)^3/2 est égale à 3/2 . Seulement j’ai utilisé des encadrements faisant intervenir l’inégalité de Bernoulli au lieu du DL.
Maintenant je serais curieuse de connaitre une méthode non classique. Cela pourrait élargir mon savoir. Merci d’avance.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
