Régression parabolique non triviale

[leon1789]

je pense que la formule de distance de Ben est fausse

Les formules de Ben (pour la fonction de t à minimiser, et pour le calcul de a) ne sont pas fausses.
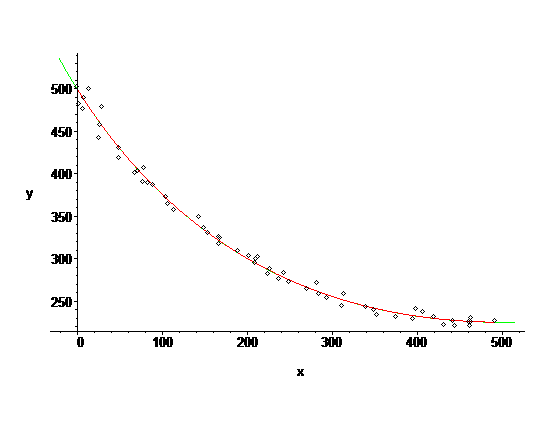
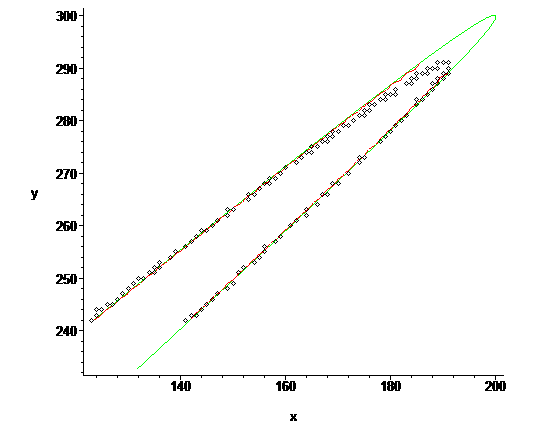
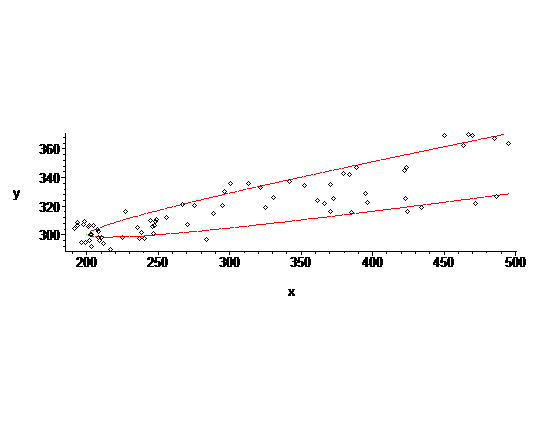
Elles ne donnent pas une distance entre les points et la parabole dans le plan, c'est plus compliqué que cela, c'est lié à une régression.

J'avoue que je ne comprends pas pourquoi tu n'arrives pas à implémenter ceci :
1/ La méthode de Lycéen permet d'obtenir une approximation t0 de l'angle de l'axe,
2/ on en déduit un intervalle [t0 - 0.5 ; t0 + 0.5 ] en radian dans lequel chercher le "vrai" angle t : au lieu de cherche dans [0, Pi] tout entier, cet intervalle réduit permet de cerner le "vrai" t
3/ La méthode de Ben (fonction à minimiser sur [t0 - 0.5 ; t0 + 0.5 ] ) permet de trouver t,
4/ puis le coefficient a

Tu as déjà écrit les points 2/ 3/ 4/ (les plus difficiles) et le point 1/ est simple : un point A sur branche, un second B sur l'autre branche, les deux à peu près à la même distance du sommet S (tu as le choix pour trouver de tels paires de points !) et le milieu M de [A, B]. Alors t0 =arctan(u /v) où (u,v) sont les coordonnées du vecteur SM

[sylvain231]

j'y suis arrivé j'en suis rendu au brute force mais je n'arrive pas à résoudre une équation du troisième degré, les formules de https://fr.wikipedia.org/wiki/M%C3%A9thode_de_Cardan sont-elles justes ? car j'en doute !

[leon1789]

Elles sont très probablement correctes, mais il y a peut-être des sous-entendus sur les racines carrées et surtout les racines cubiques avec les nombres complexes. Je me comprends...

Au lieu de faire une résolution algébrique avec ces formules, je pense que tu ferais mieux de cerner numériquement (ie par une méthode numérique, genre dichotomie ou autre plus rapide) une solution réelle de ton équation de degré 3, puis en déduire une équation de degré 2 "présentant" les deux autres solutions.

Pourquoi pas ouvrir un sujet pour aborder ce problème.

[lyceen95]

Pourquoi pas ouvrir un sujet pour aborder ce problème.

Effectivement !
18 pages pour une question, c'est beaucoup. Il y a certainement des sous-questions , des sous-projets autonomes.

[sylvain231]

ok je vais ouvrir un second thread pour cette question
une fois qu'on aura réglé ce problème je pourrais activer le brute force et on aura gagné !

[sylvain231]

j'ai vu une grave erreur dans mon code de brute force voici la ligne corrigée vous comprendrez :
Parabole PP(180*t/CV_PI, aa, sommet);

[sylvain231]

après ce changement et la correction du code de résolution d'équation de troisième degré la méthode de lyceen marche sur mon exemple, j'essaie sur d'autres exemples

[sylvain231]

non ça ne marche pas sur tous les autres exemples, le calcul de distances n'est pas bon je viens de vérifier, la résolution des équations du troisième degré fonctionne j'ai vérifié donc c'est mon code de distance qui ne fonctionne pas, vous pouvez le relire et me dire si vous voyez des erreurs SVP ?

Code: Tout sélectionner

double Parabole::distance(Point2d point) {
    double X = point.x - sommet.x;
    double Y = point.y - sommet.y;
    X = X * cos(theta_radians) - Y * sin(theta_radians);
    Y = X * sin(theta_radians) + Y * cos(theta_radians);
    vector<double> res = resoutEquationTroisiemeDegre(2 * pow(a, 2),0, 1 - 2 * a * Y, -X);
    double minimum = std::numeric_limits<double>::infinity();
    for (int k = 0; k < res.size(); k++) {//pour chaque solution complexe
        double t = res[k];
        double delta = pow(t - X, 2) + pow(a * pow(t, 2) - Y, 2);
        if (delta < minimum)
            minimum = delta;
    }
    return sqrt(minimum);
   
}

[sylvain231]

ou alors me donner un theta_radians et un a de parabole et un point assez éloigné du sommet (car ça marche plutôt bien près du sommet) et la valeur de distance attendue que je teste
s'il le faut je crée un nouveau sujet "calculer distance point parabole"

[sylvain231]

maintenant que j'ai corrigé mon calcul de distances la méthode de lyceen fonctionne dans tous les cas !
merci à vous tous de votre patience et de votre aide précieuse !
la page est tournée !

[leon1789]

Bonjour
Message tardif, mais on ne sait jamais.

A minimiser sous contrainte (en considérant theta connu) :

En fait, a²+b²=1 n'est pas la bonne contrainte pour minimiser. Comme ni a ni b ne peuvent être nuls, j'ai pris ab=1 , et là, les formules sont plus simples et les résultats absolument corrects sur tous les exemples donnés par Sylvain.

Xt := cos(t)*X-sin(t)*Y :
Yt := sin(t)*X+cos(t)*Y :

On pose comme avant
E40 := add(Xt[i]^4, i=1..n) :
E21 := add(Xt[i]^2 * Yt[i], i=1..n) :
E02 := add(Yt[i]^2, i=1..n) :

et la fonction en t à minimiser sur l'intervalle [-Pi, Pi]
f := ( E40*E02 )^(1/2) - E21 :

Pour cette valeur de t minimisante, on pose
a := (E02/E40)^(1/4)
b := (E40/E02)^(1/4)
(racine 4ième = racine carrée de la racine carrée,
a et b sont bien inverses l'un de l'autre,
et positifs, d'où bien faire attention à recherche t entre -Pi et Pi : pas de symétrie par rapport à 0)

et la parabole cherchée (sommet en (0,0)) est
0 = a * ( cos(t) * x - sin(t) * y ) ^2 - b * ( sin(t) * x + cos(t) * y )

[leon1789]

Pour

Code: Tout sélectionner

[491.147, 227.655],
 [462.454, 226.516],
 [461.672, 221.156],
 [460.218, 226.467],
 [462.521, 230.463],
 [444.12, 221.053],
 [441.868, 226.97],
 [431.279, 222.414],
 [418.907, 231.843],
 [405.601, 237.204],
 [397.975, 241.513],
 [394.867, 229.847],
 [374.528, 231.399],
 [352.032, 234.525],
 [348.5, 239.83],
 [339.034, 243.823],
 [311.215, 245.222],
 [313.473, 258.737],
 [293.544, 253.98],
 [281.78, 272.452],
 [283.286, 259.333],
 [269.725, 264.518],
 [241.851, 283.36],
 [247.822, 272.862],
 [225.791, 288.793],
 [236.361, 276.347],
 [223.803, 282.513],
 [209.34, 300.063],
 [211.769, 302.712],
 [208.739, 295.447],
 [201.1, 303.362],
 [188.385, 310.076],
 [165.963, 317.603],
 [167.426, 324.559],
 [165.749, 325.947],
 [152.545, 331.089],
 [147.793, 336.425],
 [142.001, 349.469],
 [112.913, 358.083],
 [103.538, 373.49],
 [105.365, 364.987],
 [87.9376, 387.12],
 [81.5266, 389.234],
 [76.6091, 390.403],
 [70.4323, 403.594],
 [77.5446, 407.94],
 [66.4278, 402.054],
 [47.4416, 419.374],
 [48.0166, 431.14],
 [25.2166, 458.267],
 [24.2721, 442.828],
 [27.8463, 479.668],
 [5.51483, 477.176],
 [6.52717, 490.404],
 [0.633008, 483.01],
 [12.2893, 499.955],
 [-1.9699, 503.112]

sommet en (200,300)

[sylvain231]

Bonjour et quelle est l’équation de l’ancien a en fonction des nouveaux a et b stp ?
je parle de cette équation (l'ancienne) :
0 = a * (cos(theta) * (x-sommet.x) - sin(theta) * (y-sommet.y))^2- sin(theta) * (x - sommet.x) - cos(theta) * (y - sommet.y)

[leon1789]

Pour

Code: Tout sélectionner

[141, 242],
 [123, 242],
 [142, 243],
 [143, 243],
 [124, 243],
 [124, 244],
 [144, 244],
 [144, 244],
 [125, 244],
 [126, 245],
 [145, 245],
 [145, 245],
 [127, 245],
 [128, 246],
 [146, 246],
 [146, 246],
 [129, 247],
 [147, 247],
 [147, 247],
 [130, 248],
 [149, 248],
 [131, 249],
 [150, 249],
 [150, 249],
 [132, 250],
 [133, 250],
 [151, 251],
 [134, 251],
 [151, 251],
 [135, 251],
 [135, 252],
 [152, 252],
 [152, 252],
 [136, 252],
 [136, 253],
 [154, 253],
 [154, 253],
 [138, 254],
 [155, 254],
 [139, 255],
 [139, 255],
 [156, 255],
 [156, 256],
 [141, 256],
 [141, 256],
 [158, 257],
 [158, 257],
 [142, 257],
 [143, 258],
 [159, 258],
 [159, 258],
 [144, 259],
 [144, 259],
 [145, 259],
 [161, 260],
 [161, 260],
 [146, 260],
 [146, 260],
 [147, 261],
 [162, 261],
 [162, 261],
 [162, 261],
 [149, 262],
 [164, 262],
 [164, 263],
 [149, 263],
 [164, 263],
 [150, 263],
 [150, 263],
 [166, 264],
 [166, 264],
 [166, 264],
 [153, 265],
 [153, 265],
 [153, 266],
 [167, 266],
 [168, 266],
 [154, 266],
 [168, 266],
 [154, 266],
 [155, 267],
 [155, 267],
 [155, 267],
 [156, 268],
 [169, 268],
 [169, 268],
 [156, 268],
 [170, 268],
 [170, 268],
 [157, 268],
 [157, 268],
 [157, 269],
 [158, 269],
 [158, 269],
 [159, 270],
 [172, 270],
 [172, 270],
 [159, 270],
 [172, 270],
 [172, 270],
 [159, 270],
 [160, 271],
 [162, 272],
 [162, 272],
 [174, 272],
 [174, 272],
 [174, 272],
 [163, 273],
 [174, 273],
 [175, 273],
 [175, 273],
 [163, 273],
 [163, 273],
 [164, 274],
 [165, 274],
 [165, 275],
 [166, 275],
 [167, 276],
 [178, 276],
 [178, 276],
 [167, 276],
 [178, 276],
 [178, 276],
 [178, 276],
 [168, 276],
 [178, 276],
 [179, 277],
 [179, 277],
 [168, 277],
 [179, 277],
 [179, 277],
 [179, 277],
 [179, 277],
 [179, 277],
 [169, 277],
 [179, 277],
 [179, 277],
 [179, 277],
 [169, 278],
 [180, 278],
 [180, 278],
 [180, 278],
 [180, 278],
 [180, 278],
 [170, 278],
 [180, 278],
 [171, 279],
 [171, 279],
 [181, 279],
 [181, 279],
 [181, 279],
 [181, 279],
 [172, 279],
 [181, 279],
 [181, 279],
 [182, 280],
 [182, 280],
 [182, 280],
 [173, 280],
 [182, 280],
 [182, 280],
 [182, 280],
 [182, 280],
 [182, 280],
 [173, 280],
 [182, 280],
 [182, 280],
 [183, 281],
 [174, 281],
 [183, 281],
 [183, 281],
 [174, 281],
 [183, 281],
 [183, 281],
 [183, 281],
 [175, 281],
 [175, 282],
 [176, 282],
 [176, 283],
 [177, 283],
 [177, 283],
 [185, 283],
 [185, 283],
 [185, 283],
 [185, 284],
 [186, 284],
 [178, 284],
 [186, 284],
 [178, 284],
 [179, 284],
 [179, 285],
 [180, 285],
 [187, 285],
 [187, 285],
 [180, 285],
 [187, 285],
 [187, 285],
 [180, 285],
 [181, 285],
 [181, 286],
 [188, 286],
 [188, 286],
 [188, 286],
 [188, 286],
 [188, 287],
 [189, 287],
 [183, 287],
 [189, 287],
 [183, 287],
 [184, 287],
 [189, 288],
 [184, 288],
 [189, 288],
 [184, 288],
 [189, 288],
 [185, 288],
 [190, 288],
 [190, 288],
 [185, 288],
 [185, 289],
 [190, 289],
 [185, 289],
 [190, 289],
 [190, 289],
 [186, 289],
 [190, 289],
 [186, 289],
 [190, 289],
 [186, 289],
 [190, 289],
 [187, 289],
 [190, 289],
 [187, 289],
 [191, 289],
 [187, 290],
 [191, 290],
 [187, 290],
 [191, 290],
 [187, 290],
 [191, 290],
 [188, 290],
 [191, 290],
 [188, 290],
 [191, 290],
 [188, 290],
 [191, 290],
 [188, 290],
 [189, 290],
 [191, 290],
 [189, 291],
 [191, 291],
 [189, 291],
 [191, 291],
 [189, 291],
 [191, 291],
 [189, 291],
 [191, 291],
 [191, 291],
 [190, 291],
 [191, 291],
 [191, 291],
 [190, 291],
 [190, 291],
 [191, 291],
 [191, 291],
 [190, 291],
 [190, 291],
 [191, 291],
 [191, 291]


sommet en (200,300)

[leon1789]

Pour

Code: Tout sélectionner

[267.482, 285.125],
 [270.767, 288.156],
 [279.041, 281.463],
 [297.873, 287.311],
 [296.95, 278.617],
 [300.955, 281],
 [271.478, 291.526],
 [308.361, 284.636],
 [312.525, 288.363],
 [256.566, 288.298],
 [312.581, 287.3],
 [261.177, 292.503],
 [259.556, 279.944],
 [313.525, 279.519],
 [264.735, 294.106],
 [314.178, 294.834],
 [245.998, 281.875],
 [324.267, 286.539],
 [251.241, 283.043],
 [247.328, 294.931],
 [330.708, 280.901],
 [247.969, 279.694],
 [326.908, 278.465],
 [245.711, 286.321],
 [240.133, 280.027],
 [329.768, 296.736],
 [248.547, 294.807],
 [341.837, 292.7],
 [335.604, 277.726],
 [248.832, 292.95],
 [344.93, 296.523],
 [227.99, 297.168],
 [350.353, 286.725],
 [233.201, 288.092],
 [362.114, 278.857],
 [227.542, 294.123],
 [366.041, 290.84],
 [230.65, 283.977],
 [226.301, 297.004],
 [360.336, 285.247],
 [374.28, 282.959],
 [234.264, 285.711],
 [236.231, 287.489],
 [359.8, 278.9],
 [222.586, 294.937],
 [367.932, 289.673],
 [225.639, 285.616],
 [371.935, 279.974],
 [218.128, 280.043],
 [222.87, 279.895],
 [383.229, 290.114],
 [395.42, 285.705],
 [221.632, 299.671],
 [392.265, 293.834],
 [391.034, 281.913],
 [223.666, 284.68],
 [212.066, 299.573],
 [401.484, 283.612],
 [212.072, 288.658],
 [415.035, 284.583],
 [222.008, 285.454],
 [218.825, 292.231],
 [407.697, 299.358],
 [211.833, 301.132],
 [413.215, 281.647],
 [205.717, 298.745],
 [207.695, 297.523],
 [414.048, 287.043],
 [211.844, 299.872],
 [212.759, 282.816],
 [416.342, 301.338],
 [423.256, 291.924],
 [208.061, 298.804],
 [438.614, 293.92],
 [431.543, 288.965],
 [438.403, 293.146],
 [431.161, 286.239],
 [450.916, 291.396],
 [211.25, 294.032],
 [210.966, 289.622],
 [449.317, 285.215],
 [443.112, 295.719],
 [453.402, 300.993],
 [207.455, 293.061],
 [208.529, 291.364],
 [213.392, 304.663],
 [200.486, 287.087],
 [480.236, 291.841],
 [196.158, 300.716],
 [207.314, 299.155],
 [482.622, 305.217],
 [484.274, 305.396],
 [200.374, 301.177],
 [202.411, 292.301],
 [482.002, 291.443],
 [200.144, 303.281],
 [203.505, 306.447],
 [482.737, 291.867],
 [193.109, 303.664],
 [500.254, 299.925],
 [198.549, 300.557],
 [503.011, 291.274],
 [201.566, 290.327],
 [191.766, 293.79],
 [201.34, 308.187],
 [196.012, 306.33],
 [207.89, 305.62],
 [206.46, 308.99],
 [192.98, 299.776],
 [206.256, 302.84],
 [207.823, 311.247],
 [205.701, 310.005],
 [206.973, 311.493],
 [194.84, 313.51],
 [207.34, 314.717],
 [212.993, 312.28],
 [198.166, 319.767],
 [200.617, 306.003],
 [204.75, 319.95],
 [212.673, 310.185],
 [208.976, 319.994],
 [202.67, 321.019],
 [206.421, 308.965],
 [217.924, 308.631],
 [209.052, 306.252],
 [204.235, 310.981],
 [213.244, 304.967],
 [215.96, 305.491],
 [214.196, 304.961],
 [211.805, 305.767],
 [212.828, 319.209],
 [211.973, 318.979],
 [206.937, 325.574],
 [221.408, 320.187],
 [222.701, 310.429],
 [211.348, 317.789],
 [228.102, 322.596],
 [228.357, 326.18],
 [218.2, 318.81],
 [224.679, 326.736],
 [218.712, 324.204],
 [231.277, 315.864],
 [216.799, 316.763],
 [224.554, 323.022],
 [221.09, 332.011],
 [226.868, 322.045],
 [222.381, 332.471],
 [234.031, 324.791],
 [244.863, 326.893],
 [246.266, 320.569],
 [230.009, 324.407],
 [248.026, 328.286],
 [234.652, 339.021],
 [240.475, 326.302],
 [246.63, 332.16],
 [258.97, 331.047],
 [254.178, 335.346],
 [269.673, 329.477],
 [261.492, 342.916],
 [266.265, 332.608],
 [276.594, 344.054],
 [270.005, 344.092],
 [274.673, 350.974],
 [286.818, 349.891],
 [284.758, 347.257],
 [282.444, 351.998],
 [286.284, 335.915],
 [277.264, 348.244],
 [287.799, 337.497],
 [285.46, 345.831],
 [291.811, 340.665],
 [308.726, 346.951],
 [296.154, 359.792],
 [301.711, 357.62],
 [318.017, 358.877],
 [321.479, 354.404],
 [315.924, 362.266],
 [324.928, 350.587],
 [328.778, 364.563],
 [333.935, 355.975],
 [335.449, 350.727],
 [343.1, 354.779],
 [333.89, 354.862],
 [332.888, 355.435],
 [334.498, 372.022],
 [336.535, 367.462],
 [346.141, 368.725],
 [346.866, 372.731],
 [344.535, 375.471],
 [351.613, 360.781],
 [364.466, 376.102],
 [371.239, 367.614],
 [377.703, 380.301],
 [366.553, 363.81],
 [390.86, 371.134],
 [376.333, 387.168],
 [394.05, 380.387],
 [388.948, 376.592],
 [407.356, 374.739],
 [398.114, 384.353],
 [401.716, 376.877],
 [422.619, 376.088],
 [408.631, 383.479],
 [411.149, 379.654],
 [425.453, 395.791],
 [423.555, 379.449],
 [427.992, 399.568],
 [435.561, 401.473],
 [432.725, 389.115],
 [448.947, 385.852],
 [467.686, 393.596],
 [457.138, 392.665],
 [458.754, 406.317],
 [478.914, 410.185],
 [487.105, 404.066],
 [475.926, 409.209],
 [481.975, 412.716],
 [489.667, 406.101],
 [473.577, 398.661],
 [480.364, 404.728],
 [479.291, 403.739],
 [487.364, 416.235],
 [493.849, 413.834]


sommet en (200,300)

[leon1789]

Bonjour et quelle est l’équation de l’ancien a en fonction des nouveaux a et b stp ?
je parle de cette équation (l'ancienne) :
0 = a * (cos(theta) * (x-sommet.x) - sin(theta) * (y-sommet.y))^2- sin(theta) * (x - sommet.x) - cos(theta) * (y - sommet.y)

"ancien" a = "nouveaux" a / b = ( E02 / E40 )^(1/2)

[sylvain231]

OK merci je vais tester ce soir car c'est vrai que si la méthode de lyceen marche elle est très gourmande en temps car brute force

[Ben314]

En fait, a²+b²=1 n'est pas la bonne contrainte pour minimiser. Comme ni a ni b ne peuvent être nuls, j'ai pris ab=1 , et là, les formules sont plus simples et les résultats absolument corrects sur tous les exemples donnés par Sylvain.

Tu as une idée de pourquoi ça marche mieux ?
Sachant que, le cas , signifie qu'on considère que la distance de à la parabole est alors que le cas signifie que la distance est .

Dans un cas comme dans l'autre, je vois pas bien à quoi ça correspond géométriquement . . .

[leon1789]

Pour

Code: Tout sélectionner

[202.55, 300.401],
[204.664, 306.736],
[208.678, 295.852],
[203.028, 291.776],
[216.623, 289.748],
[203.014, 299.954],
[197.975, 306.908],
[235.505, 305.353],
[240.204, 297.416],
[225.05, 297.851],
[207.399, 303.646],
[201.553, 306.371],
[236.984, 297.103],
[193.354, 308.415],
[244.705, 310.29],
[191.203, 304.652],
[202.177, 296.045],
[245.734, 306.002],
[238.153, 301.42],
[246.781, 300.924],
[248.659, 310.395],
[247.307, 306.44],
[201.266, 305.708],
[193.236, 306.229],
[198.788, 294.878],
[211.842, 293.96],
[255.991, 312.111],
[195.93, 294.657],
[198.265, 309.247],
[208.242, 302.406],
[270.47, 307.42],
[283.832, 296.533],
[208.039, 298.055],
[288.692, 315.087],
[210.432, 298.317],
[325.094, 319.051],
[227.066, 316.031],
[248.261, 308.95],
[361.271, 323.896],
[366.271, 322.137],
[372.789, 325.268],
[385.449, 315.275],
[370.391, 316.178],
[267.015, 321.102],
[394.935, 328.532],
[396.128, 322.581],
[275.113, 320.374],
[422.954, 325.092],
[424.477, 316.54],
[300.43, 336.02],
[434.116, 319.33],
[294.644, 320.411],
[296.493, 330.57],
[321.379, 332.753],
[472.012, 322.071],
[312.976, 335.645],
[486.986, 326.467],
[330.879, 326.325],
[341.902, 337.084],
[352.284, 334.586],
[370.271, 335.267],
[379.755, 343.1],
[384.096, 342.293],
[388.992, 347.203],
[422.226, 345.177],
[423.724, 346.961],
[450.314, 369.318],
[463.542, 362.208],
[469.757, 369.424],
[466.886, 370.204],
[485.574, 367.42],
[495.365, 363.63]


sommet en (200,300)

[leon1789]

Tu as une idée de pourquoi ça marche mieux ?

Non.

Dans un cas comme dans l'autre, je vois pas bien à quoi ça corresponde géométriquement . . .

Moi non plus. C'est en cherchant des trucs algébriques (bases de Gröbner...) que je me suis mis à considérer ab=1 pour indiquer que a et b sont non nuls et obtenir certaines relations plus simples.
Et puis, comme on cherche surtout le ratio a/b , je me suis dit intuitivement que normaliser a*b est peut-être plus "efficace" que normaliser a²+b².