Régression parabolique non triviale

[sylvain231]

je pense qu'à la fin je vais garder les 3 algos, les 2 qu'à cité leon plus celui de lyceen et selon les applications j'utiliserai l'un ou l'autre

[leon1789]

montre moi ton algo où il y a
this->c = E2 / E3;

superieur/regression-parabolique-non-triviale-t278846-160.html#p1549064
tu le vois ?

teste le sur les paraboles serrées.

[sylvain231]

je l'ai malheureusement supprimé mais je peux peut-être le retrouver dans les messages
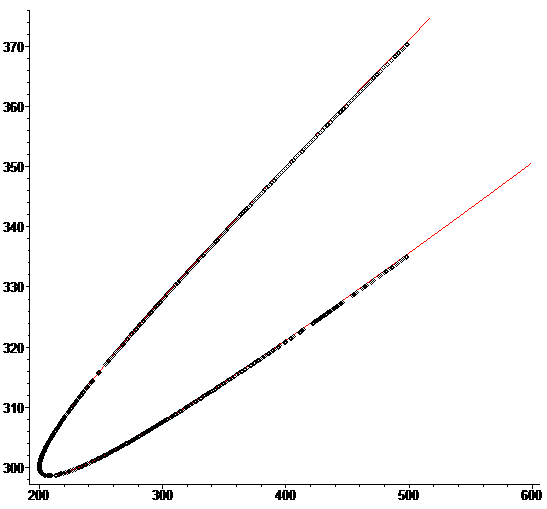
voici un exemple de parabole avec les branches séparées (sommet (200,300)) :

Code: Tout sélectionner

gauche =
[199.9, 300]
[200, 300]
[199.9, 300.1]
[200, 300.1]
[200, 300.2]
[200, 300.3]
[200.1, 300.3]
[200, 300.4]
[200.1, 300.4]
[200.1, 300.5]
[200.2, 300.5]
[200.2, 300.6]
[200.3, 300.7]
[200.4, 300.8]
[200.5, 300.9]
[200.6, 301]
[200.7, 301.1]
[200.8, 301.1]
[200.8, 301.2]
[200.9, 301.2]
[201, 301.3]
[201.1, 301.4]
[201.2, 301.4]
[201.3, 301.5]
[201.5, 301.6]
[201.6, 301.7]
[201.7, 301.7]
[201.8, 301.8]
[202, 301.9]
[202.2, 302]
[202.4, 302.1]
[202.6, 302.2]
[202.8, 302.3]
[203, 302.4]
[203.2, 302.5]
[203.4, 302.6]
[203.5, 302.6]
[203.7, 302.7]
[203.9, 302.8]
[204.1, 302.9]
[204.4, 303]
[204.6, 303.1]
[204.8, 303.2]
[204.9, 303.2]
[205.1, 303.3]
[205.3, 303.4]
[205.4, 303.4]
[205.6, 303.5]
[205.9, 303.6]
[206.1, 303.7]
[206.4, 303.8]
[206.6, 303.9]
[206.9, 304]
[207.2, 304.1]
[207.5, 304.2]
[207.7, 304.3]
[208, 304.4]
[208.3, 304.5]
[208.6, 304.6]
[208.9, 304.7]
[209.2, 304.8]
[209.4, 304.9]
[209.7, 305]
[210, 305.1]
[210.3, 305.2]
[210.6, 305.3]
[210.9, 305.4]
[211.2, 305.5]
[211.5, 305.6]
[211.8, 305.7]
[212.5, 305.9]
[212.8, 306]
[213.1, 306.1]
[213.4, 306.2]
[213.7, 306.3]
[214, 306.4]
[214.4, 306.5]
[214.7, 306.6]
[215, 306.7]
[215.3, 306.8]
[216, 307]
[216.3, 307.1]
[217, 307.3]
[217.3, 307.4]
[218, 307.6]
[218.3, 307.7]
[219, 307.9]
[219.3, 308]
[219.7, 308.1]
[220, 308.2]
[220.4, 308.3]
[220.7, 308.4]
[221.4, 308.6]
[222.1, 308.8]
[222.8, 309]
[223.2, 309.1]
[223.5, 309.2]
[223.9, 309.3]
[224.2, 309.4]
[224.6, 309.5]
[225.3, 309.7]
[225.7, 309.8]
[226, 309.9]
[226.4, 310]
[227.1, 310.2]
[227.5, 310.3]
[228.2, 310.5]
[228.6, 310.6]
[229.3, 310.8]
[229.7, 310.9]
[230.4, 311.1]
[230.8, 311.2]
[231.2, 311.3]
[231.9, 311.5]
[232.3, 311.6]
[232.7, 311.7]
[233.4, 311.9]
[233.8, 312]
[234.2, 312.1]
[235.3, 312.4]
[235.7, 312.5]
[236.1, 312.6]
[236.5, 312.7]
[237.6, 313]
[238, 313.1]
[238.4, 313.2]
[238.8, 313.3]
[240.7, 313.8]
[241.1, 313.9]
[241.5, 314]
[241.9, 314.1]
[242.3, 314.2]
[242.7, 314.3]
[243.1, 314.4]
[247.8, 315.6]
[248.2, 315.7]
[248.6, 315.8]
[253.9, 317.1]
[254.3, 317.2]
[254.7, 317.3]
[255.1, 317.4]
[255.5, 317.5]
[255.9, 317.6]
[256.3, 317.7]
[258.8, 318.3]
[259.2, 318.4]
[259.6, 318.5]
[260, 318.6]
[262.1, 319.1]
[262.5, 319.2]
[262.9, 319.3]
[264.6, 319.7]
[265, 319.8]
[265.4, 319.9]
[267.1, 320.3]
[267.5, 320.4]
[267.9, 320.5]
[269.2, 320.8]
[269.6, 320.9]
[271.3, 321.3]
[271.7, 321.4]
[273, 321.7]
[273.4, 321.8]
[274.7, 322.1]
[275.1, 322.2]
[276.4, 322.5]
[276.8, 322.6]
[278.1, 322.9]
[278.5, 323]
[279.8, 323.3]
[280.2, 323.4]
[281.1, 323.6]
[281.5, 323.7]
[282.8, 324]
[284.1, 324.3]
[284.5, 324.4]
[285.4, 324.6]
[285.8, 324.7]
[286.7, 324.9]
[287.1, 325]
[288.4, 325.3]
[289.3, 325.5]
[289.7, 325.6]
[290.6, 325.8]
[291, 325.9]
[291.9, 326.1]
[292.3, 326.2]
[293.2, 326.4]
[294.5, 326.7]
[295.8, 327]
[296.7, 327.2]
[298, 327.5]
[298.9, 327.7]
[299.3, 327.8]
[300.2, 328]
[301.1, 328.2]
[301.5, 328.3]
[302.4, 328.5]
[303.3, 328.7]
[304.6, 329]
[305.5, 329.2]
[306.8, 329.5]
[307.7, 329.7]
[308.6, 329.9]
[310.8, 330.4]
[311.7, 330.6]
[312.6, 330.8]
[313.5, 331]
[314.8, 331.3]
[315.7, 331.5]
[316.6, 331.7]
[317.5, 331.9]
[318.4, 332.1]
[319.3, 332.3]
[320.2, 332.5]
[321.1, 332.7]
[322, 332.9]
[322.9, 333.1]
[323.8, 333.3]
[324.7, 333.5]
[325.6, 333.7]
[326.5, 333.9]
[327.4, 334.1]
[328.3, 334.3]
[329.2, 334.5]
[330.1, 334.7]
[331, 334.9]
[331.9, 335.1]
[332.8, 335.3]
[333.7, 335.5]
[336, 336]
[336.9, 336.2]
[337.8, 336.4]
[338.7, 336.6]
[341, 337.1]
[341.9, 337.3]
[342.8, 337.5]
[344.2, 337.8]
[345.1, 338]
[346, 338.2]
[347.4, 338.5]
[348.3, 338.7]
[349.2, 338.9]
[350.6, 339.2]
[351.5, 339.4]
[352.9, 339.7]
[353.8, 339.9]
[355.2, 340.2]
[356.1, 340.4]
[357.5, 340.7]
[358.4, 340.9]
[359.8, 341.2]
[360.7, 341.4]
[362.1, 341.7]
[363.5, 342]
[364.4, 342.2]
[365.8, 342.5]
[367.2, 342.8]
[368.1, 343]
[369.5, 343.3]
[370.9, 343.6]
[372.3, 343.9]
[373.7, 344.2]
[374.6, 344.4]
[376, 344.7]
[377.4, 345]
[378.8, 345.3]
[380.2, 345.6]
[381.6, 345.9]
[383, 346.2]
[384.4, 346.5]
[385.8, 346.8]
[387.2, 347.1]
[388.6, 347.4]
[390.5, 347.8]
[391.9, 348.1]
[393.3, 348.4]
[394.7, 348.7]
[396.6, 349.1]
[398, 349.4]
[399.4, 349.7]
[401.3, 350.1]
[402.7, 350.4]
[404.6, 350.8]
[406, 351.1]
[407.9, 351.5]
[409.3, 351.8]
[411.2, 352.2]
[413.1, 352.6]
[414.5, 352.9]
[416.4, 353.3]
[418.3, 353.7]
[420.2, 354.1]
[422.1, 354.5]
[424, 354.9]
[425.9, 355.3]
[427.8, 355.7]
[429.7, 356.1]
[431.6, 356.5]
[433.5, 356.9]
[434, 357]
[435.9, 357.4]
[437.8, 357.8]
[439.7, 358.2]
[440.2, 358.3]
[442.1, 358.7]
[444, 359.1]
[444.5, 359.2]
[446.4, 359.6]
[446.9, 359.7]
[448.8, 360.1]
[451.2, 360.6]
[453.6, 361.1]
[455.5, 361.5]
[456, 361.6]
[458.4, 362.1]
[460.8, 362.6]
[463.2, 363.1]
[465.6, 363.6]
[466.1, 363.7]
[468.5, 364.2]
[470.9, 364.7]
[471.4, 364.8]
[473.8, 365.3]
[474.3, 365.4]
[476.7, 365.9]
[479.6, 366.5]
[482.5, 367.1]
[485.4, 367.7]
[488.3, 368.3]
[488.8, 368.4]
[491.2, 368.9]
[491.7, 369]
[494.6, 369.6]
[495.1, 369.7]
[498, 370.3]
[498.5, 370.4]
droite =
[206.8, 298.6]
[206.9, 298.6]
[207, 298.6]
[207.1, 298.6]
[207.2, 298.6]
[207.3, 298.6]
[207.4, 298.6]
[207.5, 298.6]
[207.6, 298.6]
[207.7, 298.6]
[207.8, 298.6]
[207.9, 298.6]
[208, 298.6]
[208.1, 298.6]
[208.2, 298.6]
[208.3, 298.6]
[208.4, 298.6]
[208.5, 298.6]
[208.6, 298.6]
[208.7, 298.6]
[208.8, 298.6]
[208.9, 298.6]
[209, 298.6]
[209.1, 298.6]
[209.2, 298.6]
[209.3, 298.6]
[209.4, 298.6]
[209.5, 298.6]
[209.6, 298.6]
[209.7, 298.6]
[209.8, 298.6]
[209.9, 298.6]
[210, 298.6]
[204.3, 298.7]
[204.4, 298.7]
[204.5, 298.7]
[204.6, 298.7]
[204.7, 298.7]
[204.8, 298.7]
[204.9, 298.7]
[205, 298.7]
[212.9, 298.7]
[213, 298.7]
[213.1, 298.7]
[213.2, 298.7]
[213.3, 298.7]
[213.4, 298.7]
[213.5, 298.7]
[213.6, 298.7]
[203.2, 298.8]
[203.3, 298.8]
[203.4, 298.8]
[203.5, 298.8]
[203.6, 298.8]
[215.4, 298.8]
[215.5, 298.8]
[215.6, 298.8]
[215.7, 298.8]
[215.8, 298.8]
[215.9, 298.8]
[202.4, 298.9]
[202.5, 298.9]
[202.6, 298.9]
[202.7, 298.9]
[217.4, 298.9]
[217.5, 298.9]
[217.6, 298.9]
[217.7, 298.9]
[217.8, 298.9]
[201.8, 299]
[201.9, 299]
[202, 299]
[202.1, 299]
[219.2, 299]
[219.3, 299]
[219.4, 299]
[219.5, 299]
[201.4, 299.1]
[201.5, 299.1]
[201.6, 299.1]
[220.8, 299.1]
[220.9, 299.1]
[221, 299.1]
[221.1, 299.1]
[201, 299.2]
[201.1, 299.2]
[201.2, 299.2]
[222.4, 299.2]
[222.5, 299.2]
[222.6, 299.2]
[200.7, 299.3]
[200.8, 299.3]
[200.9, 299.3]
[223.8, 299.3]
[223.9, 299.3]
[224, 299.3]
[200.5, 299.4]
[200.6, 299.4]
[200.7, 299.4]
[225.2, 299.4]
[225.3, 299.4]
[200.3, 299.5]
[200.4, 299.5]
[200.5, 299.5]
[226.5, 299.5]
[226.6, 299.5]
[226.7, 299.5]
[200.2, 299.6]
[200.3, 299.6]
[227.8, 299.6]
[227.9, 299.6]
[200.1, 299.7]
[200.2, 299.7]
[229, 299.7]
[229.1, 299.7]
[229.2, 299.7]
[200, 299.8]
[200.1, 299.8]
[230.3, 299.8]
[230.4, 299.8]
[200, 299.9]
[200.1, 299.9]
[231.4, 299.9]
[231.5, 299.9]
[231.6, 299.9]
[200.1, 300]
[232.6, 300]
[232.7, 300]
[233.8, 300.1]
[234.9, 300.2]
[235, 300.2]
[236, 300.3]
[236.1, 300.3]
[237.1, 300.4]
[237.2, 300.4]
[238.2, 300.5]
[239.2, 300.6]
[239.3, 300.6]
[240.3, 300.7]
[241.3, 300.8]
[241.4, 300.8]
[242.3, 300.9]
[242.4, 300.9]
[243.4, 301]
[244.4, 301.1]
[245.4, 301.2]
[246.4, 301.3]
[247.4, 301.4]
[248.3, 301.5]
[248.4, 301.5]
[249.3, 301.6]
[250.3, 301.7]
[251.2, 301.8]
[251.3, 301.8]
[252.2, 301.9]
[253.1, 302]
[253.2, 302]
[254.1, 302.1]
[255, 302.2]
[255.9, 302.3]
[256, 302.3]
[256.9, 302.4]
[257.8, 302.5]
[258.7, 302.6]
[259.6, 302.7]
[260.5, 302.8]
[261.4, 302.9]
[262.3, 303]
[263.2, 303.1]
[264.1, 303.2]
[265, 303.3]
[265.9, 303.4]
[266.8, 303.5]
[267.6, 303.6]
[268.5, 303.7]
[269.4, 303.8]
[270.2, 303.9]
[270.3, 303.9]
[271.1, 304]
[272, 304.1]
[272.8, 304.2]
[273.7, 304.3]
[274.6, 304.4]
[275.4, 304.5]
[276.3, 304.6]
[277.1, 304.7]
[278, 304.8]
[278.8, 304.9]
[279.6, 305]
[280.5, 305.1]
[281.3, 305.2]
[283, 305.4]
[283.8, 305.5]
[284.6, 305.6]
[285.5, 305.7]
[286.3, 305.8]
[287.1, 305.9]
[287.9, 306]
[288.8, 306.1]
[289.6, 306.2]
[290.4, 306.3]
[291.2, 306.4]
[292, 306.5]
[292.8, 306.6]
[294.5, 306.8]
[295.3, 306.9]
[296.1, 307]
[296.9, 307.1]
[297.7, 307.2]
[298.5, 307.3]
[299.3, 307.4]
[300.1, 307.5]
[300.9, 307.6]
[301.7, 307.7]
[302.5, 307.8]
[303.3, 307.9]
[304.1, 308]
[306.4, 308.3]
[307.2, 308.4]
[308, 308.5]
[308.8, 308.6]
[309.6, 308.7]
[310.4, 308.8]
[311.9, 309]
[312.7, 309.1]
[313.5, 309.2]
[314.3, 309.3]
[315.8, 309.5]
[316.6, 309.6]
[317.4, 309.7]
[318.9, 309.9]
[319.7, 310]
[320.5, 310.1]
[322, 310.3]
[322.8, 310.4]
[324.3, 310.6]
[325.1, 310.7]
[326.6, 310.9]
[327.4, 311]
[328.1, 311.1]
[328.9, 311.2]
[330.4, 311.4]
[331.2, 311.5]
[332.7, 311.7]
[334.2, 311.9]
[335.7, 312.1]
[336.5, 312.2]
[337.2, 312.3]
[338, 312.4]
[339.5, 312.6]
[341, 312.8]
[342.5, 313]
[344, 313.2]
[345.5, 313.4]
[346.2, 313.5]
[347, 313.6]
[347.7, 313.7]
[349.2, 313.9]
[350.7, 314.1]
[352.2, 314.3]
[352.9, 314.4]
[354.4, 314.6]
[355.9, 314.8]
[356.6, 314.9]
[358.1, 315.1]
[360.3, 315.4]
[361.8, 315.6]
[362.5, 315.7]
[364, 315.9]
[364.7, 316]
[366.2, 316.2]
[366.9, 316.3]
[369.1, 316.6]
[371.3, 316.9]
[372, 317]
[374.2, 317.3]
[374.9, 317.4]
[376.4, 317.6]
[377.1, 317.7]
[377.8, 317.8]
[379.3, 318]
[380, 318.1]
[380.7, 318.2]
[382.9, 318.5]
[383.6, 318.6]
[385.8, 318.9]
[386.5, 319]
[387.2, 319.1]
[389.4, 319.4]
[390.1, 319.5]
[390.8, 319.6]
[393.7, 320]
[394.4, 320.1]
[395.1, 320.2]
[398.7, 320.7]
[399.4, 320.8]
[400.1, 320.9]
[403.7, 321.4]
[404.4, 321.5]
[405.1, 321.6]
[405.8, 321.7]
[406.5, 321.8]
[410.8, 322.4]
[411.5, 322.5]
[412.2, 322.6]
[412.9, 322.7]
[413.6, 322.8]
[414.3, 322.9]
[421.4, 323.9]
[422.1, 324]
[422.8, 324.1]
[423.5, 324.2]
[424.2, 324.3]
[424.9, 324.4]
[425.6, 324.5]
[426.3, 324.6]
[427, 324.7]
[427.7, 324.8]
[428.4, 324.9]
[429.1, 325]
[429.8, 325.1]
[430.5, 325.2]
[431.2, 325.3]
[431.9, 325.4]
[432.6, 325.5]
[433.3, 325.6]
[434, 325.7]
[434.7, 325.8]
[435.4, 325.9]
[436.1, 326]
[436.8, 326.1]
[437.5, 326.2]
[438.2, 326.3]
[438.9, 326.4]
[439.6, 326.5]
[440.3, 326.6]
[441, 326.7]
[441.7, 326.8]
[442.4, 326.9]
[443.1, 327]
[443.8, 327.1]
[444.5, 327.2]
[445.2, 327.3]
[445.9, 327.4]
[454.2, 328.6]
[454.9, 328.7]
[455.6, 328.8]
[456.3, 328.9]
[457, 329]
[457.7, 329.1]
[462.5, 329.8]
[463.2, 329.9]
[463.9, 330]
[464.6, 330.1]
[465.3, 330.2]
[469.4, 330.8]
[470.1, 330.9]
[470.8, 331]
[471.5, 331.1]
[475.6, 331.7]
[476.3, 331.8]
[477, 331.9]
[480.4, 332.4]
[481.1, 332.5]
[481.8, 332.6]
[485.2, 333.1]
[485.9, 333.2]
[486.6, 333.3]
[490, 333.8]
[490.7, 333.9]
[494.1, 334.4]
[494.8, 334.5]
[497.5, 334.9]
[498.2, 335]


[leon1789]

Pour utiliser une seule méthode (la première de Ben par exemple), il serait de partager les deux branches et lancer les calculs sur chaque branche. Il faut voir si on obtient deux paraboles très proches. Je vais voir.
Non, ce n'est pas concluant.

[leon1789]

En réunissant les deux cotés, on obtient le même bon résultat avec les deux méthodes :
t := 1.39486596
a := 0.9950154891


alors qu'en séparant les cotés, cela ne fonctionne plus.

[sylvain231]

j'ai commencé à coder la méthode de lyceen j'arrive à trouver le thêta mais comment trouver le a ?
voici mon code si vous avez besoin de voir les sous-routines dîtes-le moi :

Code: Tout sélectionner

//tri par insertion
void triPoints(vector<Point2d>& points, vector<double>& distances, bool croissant) {
    int n = points.size();
    for (int i = 0; i < n; i++) {
        double x = distances[i];
        Point2d P = points[i];
        int j = i;
        while (j > 0 && distances[j - 1] > x) {
            distances[j] = distances[j - 1];
            points[j] = points[j - 1];
            j = j - 1;
        }
        distances[j] = x;
        points[j] = P;
    }
    if (!croissant) {
        std::reverse(points.begin(), points.end());
        std::reverse(distances.begin(), distances.end());
    }
}

void Parabole::fitBranches(std::vector<cv::Point2d> gauche, std::vector<cv::Point2d> droite, cv::Point2d sommet,Mat& img) {
    //calcul des distances des points de gauche avec le sommet
    vector<double> distances_gauche;
    for (int i = 0; i < gauche.size(); i++) {
        distances_gauche.push_back(distanceP(sommet, gauche[i]));
    }
    //calcul des distances des points de droite avec le sommet
    vector<double> distances_droite;
    for (int i = 0; i < droite.size(); i++) {
        distances_droite.push_back(distanceP(sommet, droite[i]));
    }
    //tri des points à gauche selon les distances décroissantes
    triPoints(gauche, distances_gauche, false);
    //tri des points à droite selon les distances croissantes
    triPoints(droite, distances_droite, true);
    //création d'un vecteur de segments à gauche
    vector<Segment> gaucheS;
    for (int i = 0; i < gauche.size() - 1; i++) {
        gaucheS.push_back(Segment(gauche[i], gauche[i + 1]));
        gaucheS[i].draw(img, 2, Scalar(255, 0, 0));
    }
    //création d'un vecteur de segments à droite
    vector<Segment> droiteS;
    for (int i = 0; i < droite.size() - 1; i++) {
        droiteS.push_back(Segment(droite[i], droite[i + 1]));
        droiteS[i].draw(img, 2, Scalar(255,255, 0));
    }
    //recherche de la somme des distances à gauche
    double DG = 0;
    for (int i = 0; i < gaucheS.size(); i++) {
        DG += gaucheS[i].getLength();
    }
    //recherche de la somme des distances à droite
    double DD = 0;
    for (int i = 0; i < droiteS.size(); i++) {
        DG += droiteS[i].getLength();
    }
    Point2d PG = gauche[0];
    Point2d PD=droite[droite.size()-1];
    if (DG > DD) {
        //on cherche le point PG de distance DD à gauche
        double sum = 0;
        int h = 0;
        for (int i = 0; i < gaucheS.size(); i++) {
            sum += gaucheS[i].getLength();
            if (sum > DD) {//on a dépassé
                h = i;
                break;
            }
        }
        double enTrop = sum - DD;
        double alpha = gaucheS[h].getAngle();
        double c = abs(cos(alpha));
        double s = abs(sin(alpha));
        if (gaucheS[h].getA().y > gaucheS[h].getB().y)
            s -= 1;
        if (gaucheS[h].getA().x > gaucheS[h].getB().x)
            c -= 1;
        PG = Point(gaucheS[h].getA().x + c * enTrop, gaucheS[h].getA().y + s * enTrop);

    }
    else {//DG < DD
        //on cherche le point PD de distance DG à droite
        double sum = 0;
        int h = 0;
        for (int i = 0; i < droiteS.size(); i++) {
            sum += droiteS[i].getLength();
            if (sum > DG) {//on a dépassé
                h = i;
                break;
            }
        }
        double enTrop = sum - DG;
        double alpha = droiteS[h].getAngle();
        double c = abs(cos(alpha));
        double s = abs(sin(alpha));
        if (droiteS[h].getA().y < droiteS[h].getB().y)
            s -= 1;
        if (droiteS[h].getA().x < droiteS[h].getB().x)
            c -= 1;
        PG = Point(droiteS[h].getB().x + c * enTrop, droiteS[h].getB().y + s * enTrop);

    }
   
    //calcul de l'angle theta :
    Point Q = (PG + PD) / 2;
    theta_radians = atan2(Q.x - sommet.x,Q.y-sommet.y);
    theta = 180 * theta_radians / CV_PI;
    drawCross(img, PG,50, Scalar(0,255,255));
    drawCross(img, PD, 50, Scalar(0, 255, 255));
}




[sylvain231]

j'ai repris le code que tu m'as dit Léon avec c=E2/E3 et elle marche sur le plat mais pas sur le serré

voici le code pour rappel :

Code: Tout sélectionner


void Parabole::fit2(std::vector<cv::Point2d> points, cv::Point2d sommet) {
    this->sommet = sommet;
    int n = points.size();
    points = translatePoint2ds(points, sommet);
    double bestTheta = 0;
    double minimum = std::numeric_limits<double>::infinity();
    for (double theta = 0; theta <= CV_PI; theta += CV_PI / 1000) {

        vector<Point2d> rotated = rotatePoint2ds(points, theta);
        double E1 = 0;
        for (int i = 0; i < n; i++) {
            E1 += pow(rotated[i].y, 2);
        }
        double E2 = 0;
        for (int i = 0; i < n; i++) {
            E2 += pow(rotated[i].x, 2) * rotated[i].y;
        }
        double E3 = 0;
        for (int i = 0; i < n; i++) {
            E3 += pow(rotated[i].x, 4);
        }
        double delta = E1 - (pow(E2, 2) / E3);
        if (delta < minimum) {
            minimum = delta;
            bestTheta = theta;
        }
    }
    this->theta_radians = bestTheta;
    this->theta = bestTheta * 180 / CV_PI;
    vector<Point2d> rotated = rotatePoint2ds(points, bestTheta);
    double E2 = 0;
    for (int i = 0; i < n; i++) {
        E2 += pow(rotated[i].x, 2) * rotated[i].y;
    }
    double E3 = 0;
    for (int i = 0; i < n; i++) {
        E3 += pow(rotated[i].x, 4);
    }
    this->a = E2 / E3;

}


[sylvain231]

bon allé je me lance dans le calcul de la distance d'un point à la parabole soyons fous !

[sylvain231]

voilà le code de la distance :

Code: Tout sélectionner

//ax^3+bx^2+c=0
vector<complex<double>> resoutEquationTroisiemeDegre(double a, double b, double c) {
    double p = b / a;
    double q = c / a;
    double Delta = -4 * pow(p, 3) - 27 * pow(q, 2);
    complex<double> j = complex<double>(-0.5, sqrt(3)/2);
    vector<complex<double>> res;
    for (int k = 0; k <= 2; k++) {
        complex<double> u = pow(j, k) * pow(0.5 * (-q + sqrt(-Delta / 27)), 1.0 / 3.0);
        complex<double> v = pow(j, -k) * pow(0.5 * (-q - sqrt(-Delta / 27)), 1.0 / 3.0);
        res.push_back(u + v);
    }
    return res;
}


double Parabole::distance(Point2d point) {
    double X = point.x * cos(theta) - point.y * sin(theta)-sommet.x;
    double Y = point.x * sin(theta) + point.y * cos(theta)-sommet.y;
    vector<complex<double>> res = resoutEquationTroisiemeDegre(2 * pow(a, 2), 1 - 2 * a * Y, -X);
    double minimum= std::numeric_limits<double>::infinity();
    for (int k = 0; k <= 2; k++) {//pour chaque solution complexe
        if (res[k].imag() < 0.00001) {//si c'est réel
            double t = res[k].real();
            double delta = pow(t - X, 2) + pow(a * pow(t, 2) - Y, 2);
            if (delta < minimum)
                minimum = delta;
        }
    }
    return sqrt(minimum);
}


[sylvain231]

petite optimisation de la résolution des équations du troisième degré pour ne pas passer par les complexes et risquer des erreurs d'arrondis dans les parties imaginaires, merci Wikipédia (https://fr.wikipedia.org/wiki/M%C3%A9thode_de_Cardan) :

Code: Tout sélectionner

//ax^3+bx^2+c=0
vector<double> resoutEquationTroisiemeDegre(double a, double b, double c) {
    double p = b / a;
    double q = c / a;
    double Delta = -4 * pow(p, 3) - 27 * pow(q, 2);
    double tiers = 1.0 / 3.0;
    vector<double> res;
    if (Delta < 0) {
        double u = pow((-q + sqrt(-Delta / 27)) / 2, tiers);
        double v = pow((-q - sqrt(-Delta / 27)) / 2, tiers);
        res.push_back(u + v);
    }
    else
    if (Delta == 0) {
        if (p == 0 && q == 0)
            res.push_back(0);
        else {
            res.push_back(3 * q / p);
            res.push_back(-3 * q / (2 * p));
        }
    }
    else if (Delta > 0) {
        for (int k = 0; k <= 2; k++) {
            res.push_back(2 * sqrt(-p / 3) * cos(tiers * acos((3 * q / 2 * p) * sqrt(3 / -p) + 2 * k * CV_PI / 3)));
        }
    }
    return res;
}


double Parabole::distance(Point2d point) {
    double X = point.x * cos(theta) - point.y * sin(theta)-sommet.x;
    double Y = point.x * sin(theta) + point.y * cos(theta)-sommet.y;
    vector<double> res = resoutEquationTroisiemeDegre(2 * pow(a, 2), 1 - 2 * a * Y, -X);
    double minimum= std::numeric_limits<double>::infinity();
    for (int k = 0; k <= 2; k++) {//pour chaque solution complexe
        double t = res[k];
        double delta = pow(t - X, 2) + pow(a * pow(t, 2) - Y, 2);
        if (delta < minimum)
            minimum = delta;
    }
    return sqrt(minimum);
}



[sylvain231]

mais j'ai testé avec quelques points et ça ne fonctionne pas du tout par exemple avec la parabole plate si je cherche la distance au sommet ça me renvoie 488

edit : j'ai vu un premier problème j'avais mis theta au lieu de theta_radians mais ça ne marche toujours pas

edit : j'ai vu mon erreur je tournait et après je translatais au lieu de faire le contraire ça semble marcher là :

Code: Tout sélectionner

//ax^3+bx^2+c=0
vector<double> resoutEquationTroisiemeDegre(double a, double b, double c) {
    double p = b / a;
    double q = c / a;
    double Delta = -4 * pow(p, 3) - 27 * pow(q, 2);
    double tiers = 1.0 / 3.0;
    vector<double> res;
    if (Delta < 0) {
        double u = pow((-q + sqrt(-Delta / 27)) / 2, tiers);
        double v = pow((-q - sqrt(-Delta / 27)) / 2, tiers);
        res.push_back(u + v);
    }
    else
    if (Delta == 0) {
        if (p == 0 && q == 0)
            res.push_back(0);
        else {
            res.push_back(3 * q / p);
            res.push_back(-3 * q / (2 * p));
        }
    }
    else if (Delta > 0) {
        for (int k = 0; k <= 2; k++) {
            res.push_back(2 * sqrt(-p / 3) * cos(tiers * acos((3 * q / 2 * p) * sqrt(3 / -p) + 2 * k * CV_PI / 3)));
        }
    }
    return res;
}


double Parabole::distance(Point2d point) {
    double X = point.x - sommet.x;
    double Y = point.y - sommet.y;
    X = X * cos(theta_radians) - Y * sin(theta_radians);
    Y = X * sin(theta_radians) + Y * cos(theta_radians);
    vector<double> res = resoutEquationTroisiemeDegre(2 * pow(a, 2), 1 - 2 * a * Y, -X);
    double minimum= std::numeric_limits<double>::infinity();
    for (int k = 0; k < res.size(); k++) {
        double t = res[k];
        double delta = pow(t - X, 2) + pow(a * pow(t, 2) - Y, 2);
        if (delta < minimum)
            minimum = delta;
    }
    return sqrt(minimum);
}


[sylvain231]

j'ai avancé sur la fonction de lyceen j'ai réussi à calculer le a en faisant un dessin sur un papier
ça colle parfaitement aux exemples mais c'est normal ce n'est pas de la régression et ça risque de pas trop coller pour les données réelles qui ne seront pas de forme bien paraboliques mais c'est le but du brute force qui vient après, voici mon code à présent :

Code: Tout sélectionner

void Parabole::fitBranches(std::vector<cv::Point2d> gauche, std::vector<cv::Point2d> droite, cv::Point2d sommet,Mat& img) {
    this->sommet = sommet;
    //calcul des distances des points de gauche avec le sommet
    vector<double> distances_gauche;
    for (int i = 0; i < gauche.size(); i++) {
        distances_gauche.push_back(distanceP(sommet, gauche[i]));
    }
    //calcul des distances des points de droite avec le sommet
    vector<double> distances_droite;
    for (int i = 0; i < droite.size(); i++) {
        distances_droite.push_back(distanceP(sommet, droite[i]));
    }
    //tri des points à gauche selon les distances décroissantes
    triPoints(gauche, distances_gauche, false);
    //tri des points à droite selon les distances croissantes
    triPoints(droite, distances_droite, true);
    //création d'un vecteur de segments à gauche
    vector<Segment> gaucheS;
    for (int i = 0; i < gauche.size() - 1; i++) {
        gaucheS.push_back(Segment(gauche[i], gauche[i + 1]));
        //gaucheS[i].draw(img, 2, Scalar(255, 0, 0));
    }
    //création d'un vecteur de segments à droite
    vector<Segment> droiteS;
    for (int i = 0; i < droite.size() - 1; i++) {
        droiteS.push_back(Segment(droite[i], droite[i + 1]));
       // droiteS[i].draw(img, 2, Scalar(255,255, 0));
    }
    //recherche de la somme des distances à gauche
    double DG = 0;
    for (int i = 0; i < gaucheS.size(); i++) {
        DG += gaucheS[i].getLength();
    }
    //recherche de la somme des distances à droite
    double DD = 0;
    for (int i = 0; i < droiteS.size(); i++) {
        DG += droiteS[i].getLength();
    }
    Point2d PG = gauche[0];
    Point2d PD=droite[droite.size()-1];
    if (DG > DD) {
        //on cherche le point PG de distance DD à gauche
        double sum = 0;
        int h = 0;
        for (int i = 0; i < gaucheS.size(); i++) {
            sum += gaucheS[i].getLength();
            if (sum > DD) {//on a dépassé
                h = i;
                break;
            }
        }
        double enTrop = sum - DD;
        double alpha = gaucheS[h].getAngle();
        double c = abs(cos(alpha));
        double s = abs(sin(alpha));
        if (gaucheS[h].getA().y > gaucheS[h].getB().y)
            s -= 1;
        if (gaucheS[h].getA().x > gaucheS[h].getB().x)
            c -= 1;
        PG = Point(gaucheS[h].getA().x + c * enTrop, gaucheS[h].getA().y + s * enTrop);

    }
    else {//DG < DD
        //on cherche le point PD de distance DG à droite
        double sum = 0;
        int h = 0;
        for (int i = 0; i < droiteS.size(); i++) {
            sum += droiteS[i].getLength();
            if (sum > DG) {//on a dépassé
                h = i;
                break;
            }
        }
        double enTrop = sum - DG;
        double alpha = droiteS[h].getAngle();
        double c = abs(cos(alpha));
        double s = abs(sin(alpha));
        if (droiteS[h].getA().y < droiteS[h].getB().y)
            s -= 1;
        if (droiteS[h].getA().x < droiteS[h].getB().x)
            c -= 1;
        PG = Point(droiteS[h].getB().x + c * enTrop, droiteS[h].getB().y + s * enTrop);

    }
   
    //calcul de l'angle theta :
    Point Q = (PG + PD) / 2;
    theta_radians = atan2(Q.x - sommet.x,Q.y-sommet.y);
    theta = 180 * theta_radians / CV_PI;
    drawCross(img, PG,50, Scalar(0,255,255));
    drawCross(img, PD, 50, Scalar(0, 255, 255));

    //translation et rotation de PG et PD les deux points loins du sommet
    cout << PG << PD << endl;
    double XG = PG.x - sommet.x;
    double YG = PG.y - sommet.y;
    XG = XG * cos(-theta_radians) - YG * sin(-theta_radians);
    YG = XG * sin(-theta_radians) + YG * cos(-theta_radians);

    double XD = PD.x - sommet.x;
    double YD = PD.y - sommet.y;
    XD = XD * cos(-theta_radians) - YD * sin(-theta_radians);
    YD = XD * sin(-theta_radians) + YD * cos(-theta_radians);
    cout << Point(XG, YG) << Point(XD, YD) << endl;
    double alpha = angle3Points(Point(0, 0), Point(XG, YG), Point(XD, YD));
    double beta =( CV_PI - alpha )/ 2;
    //calcul de aXG^2 nommé L
    double L = XD * tan(beta);
    this->a = L / pow(XD, 2);
}


j'ai aussi corrigé le code de la distance où je faisais une rotation de theta au lieu de -theta :

Code: Tout sélectionner

double Parabole::distance(Point2d point) {
    double X = point.x - sommet.x;
    double Y = point.y - sommet.y;
    X = X * cos(-theta_radians) - Y * sin(-theta_radians);
    Y = X * sin(-theta_radians) + Y * cos(-theta_radians);
    vector<double> res = resoutEquationTroisiemeDegre(2 * pow(a, 2), 1 - 2 * a * Y, -X);
    double minimum= std::numeric_limits<double>::infinity();
    for (int k = 0; k < res.size(); k++) {
        double t = res[k];
        double delta = pow(t - X, 2) + pow(a * pow(t, 2) - Y, 2);
        if (delta < minimum)
            minimum = delta;
    }
    return sqrt(minimum);
}


[sylvain231]

maintenant je me colle au brute force

[sylvain231]

j'ai vu encore une erreur dans ma résolution d'équation du troisième degré en fait C++ renvoit NaN quand on passe un nombre négatif à la racine cubique car il y a aussi des solutions complexes, pour parer j'ai bricolé un truc voici mon code :

Code: Tout sélectionner

double racine_cubique(double d) {
    if (d > 0)
        return pow(d, 1.0 / 3);
    else
        return -pow(-d, 1.0 / 3);
}

//ax^3+bx^2+c=0
vector<double> resoutEquationTroisiemeDegre(double a, double b, double c) {
    double p = b / a;
    double q = c / a;
    double Delta = -4 * pow(p, 3) - 27 * pow(q, 2);
    double tiers = 1.0 / 3.0;
    vector<double> res;
    if (Delta < 0) {
        double u = racine_cubique((-q + sqrt(-Delta / 27)) / 2);
        double v = racine_cubique((-q - sqrt(-Delta / 27)) / 2);
        res.push_back(u + v);
    }
    else
    if (Delta == 0) {
        if (p == 0 && q == 0)
            res.push_back(0);
        else {
            res.push_back(3 * q / p);
            res.push_back(-3 * q / (2 * p));
        }
    }
    else if (Delta > 0) {
        for (int k = 0; k <= 2; k++) {
            res.push_back(2 * sqrt(-p / 3) * cos(tiers * acos((3 * q / 2 * p) * sqrt(3 / -p) + 2 * k * CV_PI / 3)));
        }
    }
    cout <<(-q - sqrt(-Delta / 27)) / 2 << endl;
    return res;
}


[sylvain231]

bon j'ai une erreur dans mon code de calcul de distance mais je n'arrive pas à voiroù si vous pouviez y jeter un oeil SVP :

Code: Tout sélectionner

//ax^3+bx^2+c=0
vector<double> resoutEquationTroisiemeDegre(double a, double b, double c) {
    double p = b / a;
    double q = c / a;
    double Delta = -4 * pow(p, 3) - 27 * pow(q, 2);
    double tiers = 1.0 / 3.0;
    vector<double> res;
    if (Delta < 0) {
        double u = racine_cubique((-q + sqrt(-Delta / 27)) / 2);
        double v = racine_cubique((-q - sqrt(-Delta / 27)) / 2);
        res.push_back(u + v);
    }
    else
        if (Delta == 0) {
            if (p == 0 && q == 0)
                res.push_back(0);
            else {
                res.push_back(3 * q / p);
                res.push_back(-3 * q / (2 * p));
            }
        }
        else if (Delta > 0) {
            for (int k = 0; k <= 2; k++) {
                complex<double> temp=complex<double>(2,0) * sqrt(-complex<double>(p,0) / complex<double>(3,0))
                    * cos(tiers * acos((3 * q / 2 * p) * sqrt(complex<double>(3,0)
                        / -complex<double>(p,0)) + 2 * k * CV_PI / 3));
                res.push_back(temp.real());
            }
        }
   // cout <<"res[0]"<< res[0] << endl;
    //cout <<"Delta" << Delta << endl;
    if (isnan(res[0]) || (res.size() > 0 && isnan(res[1])) || (res.size() > 1 && isnan(res[2])))
    {
        cout << "erreur nan" << endl;
        exit(1);
    }

    return res;
}



double Parabole::distance(Point2d point) {
    double X = point.x - sommet.x;
    double Y = point.y - sommet.y;
    X = X * cos(-theta_radians) - Y * sin(-theta_radians);
    Y = X * sin(-theta_radians) + Y * cos(-theta_radians);
    vector<double> res = resoutEquationTroisiemeDegre(2 * pow(a, 2), 1 - 2 * a * Y, -X);
    double minimum = std::numeric_limits<double>::infinity();
    for (int k = 0; k <= res.size(); k++) {//pour chaque solution complexe
        double t = res[k];
        double delta = pow(t - X, 2) + pow(a * pow(t, 2) - Y, 2);
        if (delta < minimum)
            minimum = delta;
    }
    return sqrt(minimum);
   
}

[leon1789]

Salut,
La méthode est maintenant assez claire :
La méthode de Lycéen permet d'obtenir une approximation t0 de l'angle de l'axe,
on en déduit un intervalle [t0-1 ; t0+1 ] en radian dans lequel cherche le "vrai" angle t,
La méthode de Ben permet (fonction à minimiser) de trouver t,
puis le coefficient a
Et voilà !

Je laisse tomber la recherche de bug...

Sinon j'ai un second problème : maintenant je connais le sommet et deux points de chaque branche de la parabole, ma parabole est toujours translatée et tournée, comment trouver le theta et le a SVP ?

Je viens de m'apercevoir qu'il existe 3 paraboles passant par 2 points donnés (sommet fixé en (0,0) ) :

Mais bien sûr, une seule possède un point dans chaque branche (la bleue).

[sylvain231]

mais dans ma recherche de distance je dois tourner d'un angle - theta ou theta ?
et d'autre part je pense que la formule de distance de Ben est fausse car j'ai relu et relu mon code et ne vois plus d'erreur

[sylvain231]

si tu ne peux pas me déboguer ma fonction de distance ce que je comprends car c'est du C++ et tu ne connais sans doute pas le C++ tu peux par contre me donner des équations du troisième degré à résoudre avec différentes valeurs de Delta pour voir si cette fonction marche bien et après des équations de paraboles (avec theta en degré et a) et des points et leur distance pour tester cette fonction.

[sylvain231]

ah j'ai trouvé c'est mon p et mon q qui ne sont pas bons cf :
https://www.lucaswillems.com/fr/article ... ieme-degre

[sylvain231]

non ça ne marche pas non plus il faut tester avec des exemples pour valider cette fonction
voici mon code :

Code: Tout sélectionner

//ax^3+bx^2+cx+d=0
vector<double> resoutEquationTroisiemeDegre(double a, double b, double c,double d) {
    double p = (3*a*c-pow(b,2))/(3*pow(a,2));
    double q =(2*pow(b,3)-9*a*b*c+27*pow(a,2)*d)/(27*pow(a,3));
    double Delta = -4 * pow(p, 3) - 27 * pow(q, 2);
    double tiers = 1.0 / 3.0;
    vector<double> res;
    if (Delta < 0) {
        double u = racine_cubique((-q + sqrt(-Delta / 27)) / 2);
        double v = racine_cubique((-q - sqrt(-Delta / 27)) / 2);
        res.push_back(u + v);
    }
    else
        if (Delta == 0) {
            if (p == 0 && q == 0)
                res.push_back(0);
            else {
                res.push_back(3 * q / p);
                res.push_back(-3 * q / (2 * p));
            }
        }
        else if (Delta > 0) {
            for (int k = 0; k <= 2; k++) {
                complex<double> temp=complex<double>(2,0) * sqrt(-complex<double>(p,0) / complex<double>(3,0))
                    * cos(tiers * acos((3 * q / 2 * p) * sqrt(complex<double>(3,0)
                        / -complex<double>(p,0)) + 2 * k * CV_PI / 3));
                res.push_back(temp.real());
            }
        }
   // cout <<"res[0]"<< res[0] << endl;
    //cout <<"Delta" << Delta << endl;
    if (isnan(res[0]) || (res.size() > 0 && isnan(res[1])) || (res.size() > 1 && isnan(res[2])))
    {
        cout << "erreur nan" << endl;
        exit(1);
    }

    return res;
}



double Parabole::distance(Point2d point) {
    double X = point.x - sommet.x;
    double Y = point.y - sommet.y;
    X = X * cos(-theta_radians) - Y * sin(-theta_radians);
    Y = X * sin(-theta_radians) + Y * cos(-theta_radians);
    vector<double> res = resoutEquationTroisiemeDegre(2 * pow(a, 2),0, 1 - 2 * a * Y, -X);
    double minimum = std::numeric_limits<double>::infinity();
    for (int k = 0; k <= res.size(); k++) {//pour chaque solution complexe
        double t = res[k];
        double delta = pow(t - X, 2) + pow(a * pow(t, 2) - Y, 2);
        if (delta < minimum)
            minimum = delta;
    }
    return sqrt(minimum);
   
}