Bonsoir, auriez vous l'obligeance et l'amabilité de m'aider sur la résolution de cet exercice.
Soit n un entier . Quelles sont les valeurs possibles de n telles que \sqrt{n^{2}+139n+5041} est un entier ?
Merci d'avance et bonne soirée.
Suites 1ere S
11 messages
- Page 1 sur 1
Re: Suites 1ere S
Merci !
Pouvez vous m'expliquer comment vous avez trouvé ses résultats et s'il y en a d'autres ?
Merci d'avance
Pouvez vous m'expliquer comment vous avez trouvé ses résultats et s'il y en a d'autres ?
Merci d'avance
Re: Suites 1ere S
bonjour,
j 'ai fait tourner le programme suivant en Python
Jusqu'à cent millions, il n'y a que les solutions 0 et 141.
j 'ai fait tourner le programme suivant en Python
- Code: Tout sélectionner
from math import *
n=0
n=int(n)
while n < 100000000:
u=sqrt(n*n+139*n+5041)
if u == int(u): #u entier ?
print(n)
n +=1.
Jusqu'à cent millions, il n'y a que les solutions 0 et 141.
Re: Suites 1ere S
re,
le fait qu'il semble n'y avoir que deux solutions (0 et 141) et que l'on ait un polynôme de degré 2
de la variable n , conduit à un calcul avec un trinôme du second degré.
on a les conditions nécessaires:
 tel que
tel que
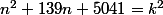
soit
=0)
On calcule le delta:
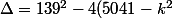)
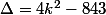
Le discriminant doit être un carré parfait:
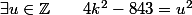
et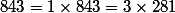
On est conduit à deux systèmes d'inconnues k et u.
je te laisse poursuivre.
le fait qu'il semble n'y avoir que deux solutions (0 et 141) et que l'on ait un polynôme de degré 2
de la variable n , conduit à un calcul avec un trinôme du second degré.
on a les conditions nécessaires:
soit
On calcule le delta:
Le discriminant doit être un carré parfait:
et
On est conduit à deux systèmes d'inconnues k et u.
je te laisse poursuivre.
Modifié en dernier par mathelot le 02 Mar 2022, 10:17, modifié 1 fois.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
