Exercice nombre complexe (racines carré, équation )
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
par novicemaths » 26 Nov 2021, 20:58
Bonsoir
Pourriez-vous s'il vous plait vérifier mes calculs.
1) Trouver les racines carrées du nombre complexe
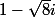
Soit
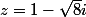
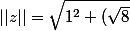^2} = \sqrt{1+8}= \sqrt{9}=3)
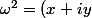^2=1-\sqrt{8}i \Longleftrightarrow x^2-y^2+2ixy = 1-\sqrt{8}i <br /> \Longleftrightarrow \begin{cases}<br /> x^2-y^2=1 \\ <br />x^2+y^2=3 \\ <br />2xy= -\sqrt{8} <br />\end{cases} \Longleftrightarrow \begin{cases}<br /> 2x^2=4 \\ <br />2y^2=2 \\ <br />xy= -\frac{\sqrt{8}}{2} <br />\end{cases})
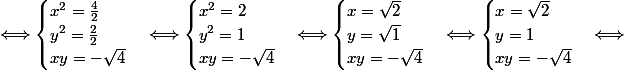
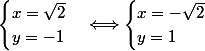
Les solutions sont
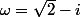
et
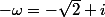
2) Utiliser (1) pour résoudre l'équation
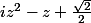Je ne vois pas comment finir le calcul avec 2i au dénominateur, je ne vois pas comment le retirer+\sqrt{2}-i}{2i} = \frac{1+\sqrt{2}-i}{2i})
-\sqrt{2}+i}{2i} = \frac{1-\sqrt{2}+i}{2i})
Merci !!
A bientôt
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
par Carpate » 26 Nov 2021, 21:26
-
mathelot
par mathelot » 26 Nov 2021, 21:27
re,
il y a une erreur dans le calcul de la racine carrée , le produit xy vaut -rac(2). sinon les résultats sont justes.
Pour simplifier le dénominateur 2i, multiplier haut et bas le quotient par -i
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
par novicemaths » 26 Nov 2021, 21:49
Je ne comprends pas pourquoi
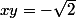
mathelot
A bientôt
-
mathelot
par mathelot » 26 Nov 2021, 22:02
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
par novicemaths » 26 Nov 2021, 22:15
Ah!!
Ok, on ne peut pas diviser les racine directement ?
Navré les calculs de base , j'essaie de les apprendre tout seul.
Est-ce que ci-dessous c'est correct ?
}{2i \times (-i)} = \frac{-i + \sqrt{2}}{2})
}{2i \times (-i)} = \frac{-i - \sqrt{2}}{2})
A bientôt
-
mathelot
par mathelot » 26 Nov 2021, 22:29
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
par novicemaths » 26 Nov 2021, 22:39
Merci mathelot.
Je vais refaire les calculs à tête reposé.
A bientôt
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
par Pisigma » 26 Nov 2021, 22:51
Bonsoir,
1) on peut arriver plus rapidement au résultat en remarquant que
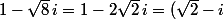^2)
d'où
^2=0)
soit
(z-\sqrt{2}+i)=0)
-
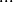
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
par tournesol » 26 Nov 2021, 23:19
Bonsoir Pisigma
Les racines carrées de A^2 sont -A et A .
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
par Pisigma » 26 Nov 2021, 23:25
Bonsoir tournesol,
je suppose que tu avais déjà remarqué que "j'aimais bien" les factorisations
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
