Récurrence

[beagle]

euh 57 marche pas
quelle conclusion donner ? :
je sais pas

"Nous n'arrivons pas à démontrer que 7^n +1 est un multiple de 6 par la méthode de récurrence" ?

[lyceen95]

Avec les calculs qui ont été faits, on peut dire : Dès qu'on trouve un nombre n tel que 7^n+1 soit un multiple de 6, alors tous les suivants sont des multiples de 6.
Dès qu'on trouve ... ça veut dire qu'on va peut-être trouver, peut-être pas.
Avec les calculs faits, on ne peut rien conclure de plus.

Avec quelques calculs pas plus compliqués que ceux qui ont été faits, on pourrait prouver que tous les nombres de la forme sont des multiples de 6. Et dont tous les 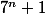sont des (6k+2) , et donc pas des multiples de 6.
Aucun de ces nombres n'est un multiple de 6.
Les calculs ne sont pas compliqués pour le prouver.

Mais, je me répète, les calculs faits pour l'instant permettent juste de dire : Si on trouve un nombre n tel que 7^n+1 serait un multiple de 6, alors les suivants sont aussi des multiples de 6, mais on ne sait pas si un tel nombre existe.

[Ben314]

ok merci
j'ai tester jusqu'à n = 55 et non

Il me semble qu'on te l'a déjà dit : en fait c'est FAUX pour tout les entiers naturels n.
Et la façon peut-être la plus simple de le voir, c'est juste d'écrire que et de voir que non seulement ça signifie que, si est multiple de 6 alors l'est aussi (c'est ça qu'on appelle l'hérédité), mais que ça marche aussi dans l'autre sens, à savoir que, si est multiple de 6 alors aussi.

Après, le sens "usuel", il te permet de voir que, si par exemple la propriété est vrai pour n=327 alors elle va l'être pour n=328. Puis que, comme elle est vrai pour n=328, alors elle va l'être pour n=329, etc
Et donc en fait, elle va l'être pour tout les entiers (et c'est ça qu'on appelle une récurrences).

Mais ça marche tout pareil dans l'autre sens avec la propriété réciproque qui, ici, est tout aussi vraie (alors que ce n'est évidement pas toujours le cas) : Le fait que, si est multiple de 6 alors aussi te dit que, si par exemple est multiple de 6 pour n=327 alors c'est aussi un multiple de 6 pour n=326 donc c'est aussi un multiple de 6 pour n=325 etc
Et donc en fait, ça signifie que c'est un multiple de 6 pour tout les entiers .

Et cette parie "réciproque", ce qu'elle te dit, c'est que si la propriété était vrai pour UN entier (n'importe lequel) alors elle serait aussi vrai pour tout les entiers qui précède cet entier. Et en particulier, elle serait vraie pour n=0.
Et, comme il s'avère qu'en fait la propriété est fausse pour n=0, ben ça veut dire qu'elle est fausse pour tout les entiers.

[beagle]

ah merci Ben314, c'est super

cela fait longtemps que je pensais à la descente de l'hérédité,
mais je ne vous voyais jamais l'utiliser dans les forums alors je me demandais s'il y avait un truc qui s'y opposerait.

[mathelot]

@maxou: ton raisonnement est correct, l'hypothèse est multiple de est héréditaire.
Comme , 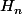est fausse quelque soit n

Exemple de propriété héréditaire et toujours fausse:
"Chez les humains ,les enfants de parents de grande taille sont de grande taille" est vraie .
Chez le peuple des pygmées, réputés pour leur petite taille, l'assertion est fausse, (et héréditaire)

[tournesol]

Bonsoir Ben314 .
Merci pour ton rappel . Le "mais" est effectivement incongru .
Quelques remarques sur la récurrence:
Lorsqu'on a demontré une hérédité ascendente à partir de a , la vérité se propage en aval et la fausseté en amont jusqu'à a , autrement dit :
si il existe b supérieur ou égal à a tel que p(b) est vraie , alors p(n) est vraie pour tout n supérieur ou égal à b .
si il existe b supérieur ou égal à a tel que p(b) est fausse , alors p(n) est fausse pour tout n compris au sens large entre a et b .
Tu as montré une hérédité descendente pour cet exo , donc la fausseté se propage aussi en aval .
Donc faux pour 0 , faux pour tout n .