Récurrence

[maxou211000]

Bonjour à tous,

[azf]

P(n): (7^n)+1 est un multiple de 6

Bonjour
n'est pas multiple de 6
c'est
qui est multiple de 6

vous avez mal recopié votre énoncé

sinon à part ça c'est évident puisque

[maxou211000]

1

[azf]

sauf que

P(n): (7^n)+1 est un multiple de 6

c'est faux (il suffit d'utiliser la formule du binôme de Newton comme dans mon post précédent pour le voir )

[maxou211000]

D'accord super merci !

[azf]

Votre énoncé est faux

P(n): (7^n)+1 est un multiple de 6

un énoncé correct par exemple aurait été

Montrer par récurrence que P(n): (7^n)+1 n'est pas un multiple de 6

L'intérêt de faire un exercice c'est de le faire sur la base d'un énoncé correct non?

comment voulez vous rien que par exemple avec n=0 que 7^0+1=1+1=2 soit un multiple de 6?

De deux choses l'une soit vous avez mal recopié votre énoncé soit c'est l'énoncé qui est mauvais

[maxou211000]

C

[tournesol]

Rassures toi , ton exercice n'est pas faux .
On ne te demande pas de montrer que P est vraie mais seulement héréditaire...et c'est immediat:
entraine
CQFD
l'intéret pédago de cet exo c'est qu'il donne un exemple de propriété fausse pour tout n mais héréditaire .

[maxou211000]

J'ai compris merci beaucoup !

[beagle]

Salut tournesol,
tu sais si cela s'utilise l'hérédité descendante
si P(n) alors P(n-1)
?

[Ben314]

Salut,

l'intéret pédago de cet exo c'est qu'il donne un exemple de propriété fausse pour tout n mais héréditaire .

Un petit rappel de logique : lorsque la proposition P est fausse, la proposition (P=>Q) est vraie, (quelque soit la valeur de vérité de Q).
Donc lorsque l'on a une suite de proposition qui sont toutes fausses, alors ça entraine mécaniquement que est vrai pour tout , c'est à dire qu'il y a obligatoirement hérédité.
Bref, le "mais" est un peu mal placé . . .

[maxou211000]

B

[Ben314]

. . . mais aucune valeur ne fonctionne

Je comprend pas de quoi tu parle : une valeur de quelle variable qui "fonctionne" pour quelle formule ?
Sinon, ce qu'on te demande de montrer, c'est que :
Si pour un entier n donné 7^n+1 est divisible par 6 alors 7^(n+1)+1 est lui aussi divisible par 6.
Et les différentes remarques des intervenant signalent uniquement que, cette implication est vraie (pour tout entier n), et que sa prémisse est fausse.

[beagle]

Bonjour maxxou

tu as démontré que si P(n) était vrai alors P(n+1) serait vrai.
Egalement tu as démontré que
quand P(n) sera vrai alors P(n+1) sera vrai

Si tu ne trouves pas un début (initialisation) vrai parce que cela n'existe pas (P(n) sera jamais vrai,
et bien c'est mort
tu n'as (heureusement) pas démontré que c'était vrai (7^n+1 multiple de 6)

C'est d'ailleurs une des raisons de commencer par l'initialisation en général dans la démonstration par récurrence!

[beagle]

Bon Ben314 c'est trop crétin de faire la récurrence descendante ?

Si j'avais P(n) vrai alors j'aurais P(n-1) qui serait vrai
or pour n= 0 ou 1 c'est faux
donc il n' y a pas de P(n) vrai

[maxou211000]

J'

[lyceen95]

Revenons à un truc plus général. La démonstration par récurrence.

Dans une démonstration par récurrence, on procède en 2 étapes :
-A-initialisation - Vérifier que la propriété est vraie pour n=0 ou n=1
-B-hérédité- Vérifier que si la propriété est vraie pour une valeur de n donnée, alors elle est forcément vraie pour la valeur de n immédiatement supérieure.

Ici, on a fait une démonstration par récurrence, ou presque.
On a bien vérifié la ligne B
Mais on n'a pas vérifié la ligne A.

L'idée (pédagogique) de l'exercice, c'est de rappeler que dans une démonstration par récurrence, il y a bien 2 étapes (A et B) (ou Initialisation et hérédité), et que B ne suffit pas. Si on vérifie la propriété B, sans avoir vérifié A, alors on en vient à dire que , , ... ... 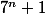sont des multiples de 6. Alors que c'est faux.

Et donc, ce qu'on te demande, c'est de rappeler que dans une démonstration par récurrence, si on ne vérifie pas l'Initialisation, la démonstration est incomplète.

[maxou211000]

D'accord

[beagle]

"que comme nous ne pouvons pas le vérifier pour un N, "
c'est ennuyeux comme phrase après avoir tester, n= 1 à 4

je pense n= 57 peut marcher

[maxou211000]

ok merci