Bonjour à tous, j'espère que vous allez bien !
J'ai du mal à comprendre une chose :
Lorsqu'on utilise des opérations sur les lignes ou les colonnes d'une matrice dans le but d'évaluer le déterminant de celle-ci, la permutation de deux lignes ou de deux colonnes change le signe du déterminant.
Cependant, lorsqu'on échelonne une matrice, permuter deux lignes ou deux colonnes ne change rien à celle-ci.
Je ne comprends pas quelle est la différence et pourquoi ça affecte l'un mais pas l'autre... Dans le cas de la résolution d'un problème, comment suis-je censée savoir si je dois utiliser une matrice ou un déterminant ? Quelle est la différence ?
Franchement c'est très flou pour moi, toute aide sera grandement appréciée.
Merci infiniment.
Matrice vs déterminant nxn
7 messages
- Page 1 sur 1
Re: Matrice vs déterminant nxn
Bonjour,
Une matrice est un tableau de nombres. Quand on fait une opération élémentaire sur les lignes d'une matrice, on change la matrice, ce n'est plus la même matrice. On obtient une matrice qui n'est pas égale à la matrice de départ, mais seulement équivalente à celle-ci (pour une relation d'équivalence qu'on appelle équivalence à gauche, parce que faire une suite d'opérations élémentaires sur les lignes d'une matrice revient à multiplier celle ci à gauche par une matrice inversible). Cette relation d'équivalence préserve un certain nombre de propriétés de la matrice, essentiellement le sous espace engendré par les lignes de la matrice, et donc le rang de cette matrice.
Le déterminant d'une matrice carrée est un nombre. Le déterminant de la matrice ne change pas quand on ajoute à une ligne un multiple d'une autre ligne. Le déterminant de la matrice est changé en son opposé quand on permute deux lignes de la matrice.
Une matrice est un tableau de nombres. Quand on fait une opération élémentaire sur les lignes d'une matrice, on change la matrice, ce n'est plus la même matrice. On obtient une matrice qui n'est pas égale à la matrice de départ, mais seulement équivalente à celle-ci (pour une relation d'équivalence qu'on appelle équivalence à gauche, parce que faire une suite d'opérations élémentaires sur les lignes d'une matrice revient à multiplier celle ci à gauche par une matrice inversible). Cette relation d'équivalence préserve un certain nombre de propriétés de la matrice, essentiellement le sous espace engendré par les lignes de la matrice, et donc le rang de cette matrice.
Le déterminant d'une matrice carrée est un nombre. Le déterminant de la matrice ne change pas quand on ajoute à une ligne un multiple d'une autre ligne. Le déterminant de la matrice est changé en son opposé quand on permute deux lignes de la matrice.
Re: Matrice vs déterminant nxn
GaBuZoMeu a écrit:Bonjour,
Une matrice est un tableau de nombres. Quand on fait une opération élémentaire sur les lignes d'une matrice, on change la matrice, ce n'est plus la même matrice. On obtient une matrice qui n'est pas égale à la matrice de départ, mais seulement équivalente à celle-ci (pour une relation d'équivalence qu'on appelle équivalence à gauche, parce que faire une suite d'opérations élémentaires sur les lignes d'une matrice revient à multiplier celle ci à gauche par une matrice inversible). Cette relation d'équivalence préserve un certain nombre de propriétés de la matrice, essentiellement le sous espace engendré par les lignes de la matrice, et donc le rang de cette matrice.
Le déterminant d'une matrice carrée est un nombre. Le déterminant de la matrice ne change pas quand on ajoute à une ligne un multiple d'une autre ligne. Le déterminant de la matrice est changé en son opposé quand on permute deux lignes de la matrice.
Merci beaucoup pour votre message !
Voici ce que je ne comprends toujours pas : Par exemple, si je veux calculer le déterminant d'une matrice, j'ai deux choix : soit je simplifie d'abord la matrice, soit je simplifie le déterminant. Si je simplifie la matrice en permutant deux lignes, rien ne change. Cependant, si je simplifie le déterminant en permutant deux lignes, le signe change. Comment est-ce qu'au final on peut arriver au même résultat alors que le déterminant sera affecté par les opérations de permutation mais pas la matrice ?
Re: Matrice vs déterminant nxn
Bonjour,
Une matrice est un tableau de nombre tandis qu'un déterminant est un nombre : ce n'est pas du tout la même chose.
Quand tu échelonnes une matrice, tu la modifies en une autre matrice qui n'a donc pas nécessairement le même déterminant. Si est ta matrice initiale et
est ta matrice initiale et  ta matrice échelonné, il existe une matrice
ta matrice échelonné, il existe une matrice  dite de passage vérifiant
dite de passage vérifiant  . En passant au déterminant on a
. En passant au déterminant on a  = det(P)det(A)) et le déterminant de
et le déterminant de  n'a aucune raison d'être égale à 1.
n'a aucune raison d'être égale à 1.
Une matrice est un tableau de nombre tandis qu'un déterminant est un nombre : ce n'est pas du tout la même chose.
Quand tu échelonnes une matrice, tu la modifies en une autre matrice qui n'a donc pas nécessairement le même déterminant. Si
Re: Matrice vs déterminant nxn
Rhaegar a écrit:Bonjour,
Une matrice est un tableau de nombre tandis qu'un déterminant est un nombre : ce n'est pas du tout la même chose.
Quand tu échelonnes une matrice, tu la modifies en une autre matrice qui n'a donc pas nécessairement le même déterminant. Siest ta matrice initiale et
ta matrice échelonné, il existe une matrice
dite de passage vérifiant
. En passant au déterminant on a
et le déterminant de
n'a aucune raison d'être égale à 1.
C'est très intéressant je n'étais pas du tout au courant ! Mais dans ce cas si j'ai un problème, par exemple un système d'équations linéaires à résoudre, est-ce que je dois réduire la matrice ou le déterminant ?
Je vous donne un exemple concret : Déterminer toutes les valeurs de k pour lesquelles le système d'équations linéaires suivant a une et une seule solution :
x + y + z - kw = 0
x + ky + 2z + w = 1
2x + ky + z + w = 2
x + ky + z + w = 3
Je sais qu'ici la réponse est tous les réels, mais si je veux résoudre ce problème, est-ce que je dois mettre les coefficients dans une matrice et réduire ou les mettre dans un déterminant et réduire ? En sachant que permuter deux lignes affectera l'un mais pas l'autre ?
Re: Matrice vs déterminant nxn
Bonjour
Comme c'est la nuit je poste une aide mais c'est à titre exceptionnel car je n'empiète pas sur les aides des autres que je salue au passage (mais ils dorment)
On vous rappelle qu'un déterminant est un nombre (il ne se réduit pas)
À toute matrice associée à un système d'équation linéaire on peut y associer une matrice dite échelonnée réduite (plus simple) et cette matrice est unique
Pour cela il faut effectuer des opération élémentaires
1.permuter deux lignes
2.Multiplier une ligne par un scalaire non nul
3.Ajouter à une ligne le produit d'une autre ligne par un scalaire
Pour obtenir cette réduction il faut faire en sorte qu'avec ces opérations on ait
1.Toutes les lignes nulles (s'il y en a) sont situées en dessous des lignes non nulles
2.Dans chaque ligne le premier coefficient non nul vaut 1
La colonne où est situé le premier le premier coefficient non nul de cette ligne est appelé colonne pivôt de cette ligne
3.La colonne pivôt d'une ligne possède que uniquement ce pivôt pour seul coefficient non nul
4.Le pivôt de toute colonne pivôt qui précède la colonne pivôt d'une ligne est toujours situé au dessus de cette ligne
par exemple
son échelonnée réduite sera
par exemple en considérant un système homogène qui matricellement s'écrit
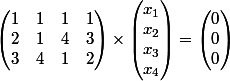
vous avez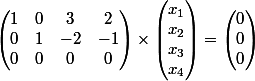
avec cette matrice là il est facile de trouver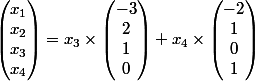
bon moi j'ai faim et là il y a de la viande (et le soleil est sur le point de se lever et dans les Carpâtes c'est pas notre truc le soleil lol)
https://www.youtube.com/watch?v=mqhbwrrfND8
Comme c'est la nuit je poste une aide mais c'est à titre exceptionnel car je n'empiète pas sur les aides des autres que je salue au passage (mais ils dorment)
sarah12345 a écrit: Mais dans ce cas si j'ai un problème, par exemple un système d'équations linéaires à résoudre, est-ce que je dois réduire la matrice ou le déterminant ?
On vous rappelle qu'un déterminant est un nombre (il ne se réduit pas)
À toute matrice associée à un système d'équation linéaire on peut y associer une matrice dite échelonnée réduite (plus simple) et cette matrice est unique
Pour cela il faut effectuer des opération élémentaires
1.permuter deux lignes
2.Multiplier une ligne par un scalaire non nul
3.Ajouter à une ligne le produit d'une autre ligne par un scalaire
Pour obtenir cette réduction il faut faire en sorte qu'avec ces opérations on ait
1.Toutes les lignes nulles (s'il y en a) sont situées en dessous des lignes non nulles
2.Dans chaque ligne le premier coefficient non nul vaut 1
La colonne où est situé le premier le premier coefficient non nul de cette ligne est appelé colonne pivôt de cette ligne
3.La colonne pivôt d'une ligne possède que uniquement ce pivôt pour seul coefficient non nul
4.Le pivôt de toute colonne pivôt qui précède la colonne pivôt d'une ligne est toujours situé au dessus de cette ligne
par exemple
son échelonnée réduite sera
par exemple en considérant un système homogène qui matricellement s'écrit
vous avez
avec cette matrice là il est facile de trouver
bon moi j'ai faim et là il y a de la viande (et le soleil est sur le point de se lever et dans les Carpâtes c'est pas notre truc le soleil lol)
https://www.youtube.com/watch?v=mqhbwrrfND8
Re: Matrice vs déterminant nxn
Bonjour,
En échelonnant ta matrice, tu fais des opérations qui ne changent pas les solutions du système linéaire. C'est pour cela qu'on échelonne pour résoudre les systèmes linéaires. Cependant le déterminant change (comme tu l'as constaté). Mais le déterminant ne donne qu'une information sur le système qui ne permet pas de le résoudre. Si le déterminant est non-nul, alors le système est de rang maximal et tu peux échelonner jusqu'au bout pour trouver une unique solution au système. Mais connaître seulement le déterminant ne t'indiquera pas quelle est cette solution. Si le déterminant est nul, le système n'est pas de rang maximal. En échelonnant, tu vas découvrir que tu as des équations en double. Au final, tu auras plus d'équations que d'inconnus. Dans ce cas, tu auras soit aucune solution, soit une infinité. Mais le déterminant ne te dis pas dans quel cas tu es et encore moins quelles sont les solutions s'il y en a. Dans mon exemple de tout à l'heure avec , le déterminant de
, le déterminant de  n'est jamais nul. Par conséquent, les déterminants de
n'est jamais nul. Par conséquent, les déterminants de  et
et  sont nuls en même temps où ne sont pas nul en même temps : les informations qu'il donne sur le système sont les mêmes. Le rang de
sont nuls en même temps où ne sont pas nul en même temps : les informations qu'il donne sur le système sont les mêmes. Le rang de  et de
et de  est le même et le solutions des systèmes associées également.
est le même et le solutions des systèmes associées également.
En s'éloignant un peu du sujet :
La valeur du déterminant lorsque celui-ci est non-nul donne d'autres informations sur la matrice (déterminant négatif si la transformation associée à A renverse l'orientation, déterminant plus ou moins grand si la transformation à tendance à étirer ou non les longueur). Ces informations ne sont pas conservées en échelonnant la matrice (car \neq 1) en général notamment) mais le solutions du systèmes linéaire si.
en général notamment) mais le solutions du systèmes linéaire si.
En fait, deux matrices et
et  sont équivalentes lorsqu'il existe une matrice de passage
sont équivalentes lorsqu'il existe une matrice de passage  vérifiant
vérifiant  . Comme
. Comme  = 1/det(P)) , on a
, on a  = det(B)) . Donc pour cette relation d'équivalence, les déterminants sont conservée. Les transformations associées à
. Donc pour cette relation d'équivalence, les déterminants sont conservée. Les transformations associées à  et
et  sont les même mais exprimées dans des bases différentes.
sont les même mais exprimées dans des bases différentes.
J'espère que tu as mieux compris et que je t'ai pas trop embrouillé avec la deuxième partie.
En échelonnant ta matrice, tu fais des opérations qui ne changent pas les solutions du système linéaire. C'est pour cela qu'on échelonne pour résoudre les systèmes linéaires. Cependant le déterminant change (comme tu l'as constaté). Mais le déterminant ne donne qu'une information sur le système qui ne permet pas de le résoudre. Si le déterminant est non-nul, alors le système est de rang maximal et tu peux échelonner jusqu'au bout pour trouver une unique solution au système. Mais connaître seulement le déterminant ne t'indiquera pas quelle est cette solution. Si le déterminant est nul, le système n'est pas de rang maximal. En échelonnant, tu vas découvrir que tu as des équations en double. Au final, tu auras plus d'équations que d'inconnus. Dans ce cas, tu auras soit aucune solution, soit une infinité. Mais le déterminant ne te dis pas dans quel cas tu es et encore moins quelles sont les solutions s'il y en a. Dans mon exemple de tout à l'heure avec
En s'éloignant un peu du sujet :
La valeur du déterminant lorsque celui-ci est non-nul donne d'autres informations sur la matrice (déterminant négatif si la transformation associée à A renverse l'orientation, déterminant plus ou moins grand si la transformation à tendance à étirer ou non les longueur). Ces informations ne sont pas conservées en échelonnant la matrice (car
En fait, deux matrices
J'espère que tu as mieux compris et que je t'ai pas trop embrouillé avec la deuxième partie.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
