Ensemble de définition des fonctions
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
John38
- Messages: 9
- Enregistré le: 27 Mai 2021, 12:15
-
 par John38 » 27 Mai 2021, 13:20
par John38 » 27 Mai 2021, 13:20
Bonjour,
Je rencontre des difficultés pour donner l'ensemble de définition des fonctions.
Voici ou je bloque :
\ =\ \frac{1}{x-1}\ \ \ \ \ \ \ \ \ \ et\ \ g(x)\ =\ x^2-3)
Déterminer l’ensemble de définition des fonctions f, g, gof et fog
J'ai trouvé pour f et g mais je ne comprends pas très bien comment faire pour gof et fog.
Je vous remercie d'avance.
-
azf
 par azf » 27 Mai 2021, 13:44
par azf » 27 Mai 2021, 13:44
Bonjour
Comme vous l'avez trouvé pour f et pour g (parce que ces fonctions sont écrites explicitement) je suis certain que si vous écrivez explicitement fog et gof vous allez trouver pour chacune d'elle l'ensemble de définition
-
azf
 par azf » 27 Mai 2021, 14:41
par azf » 27 Mai 2021, 14:41
Soit dit en passant ce n'est pas obligé
Dans ce cas vous devez trouver les ensembles d'application de f et g
D'où l'intérêt de les trouver même s'ils ne sont pas demandés
Ces quatre ensembles de définition et d'application de f et g vont vous aider à trouver ce que vous cherchez (c'est un résultat que vous avez certainement dans votre cours)
-
John38
- Messages: 9
- Enregistré le: 27 Mai 2021, 12:15
-
 par John38 » 27 Mai 2021, 15:46
par John38 » 27 Mai 2021, 15:46
Merci pour votre réponse donc je trouve

et

-
azf
 par azf » 27 Mai 2021, 15:52
par azf » 27 Mai 2021, 15:52
John38 a écrit:Merci pour votre réponse donc je trouve

mais que vaut g(2)? et que va valoir f(g(2))?
que vaut g(-2)? et que va valoir f(g(-2))?
-
John38
- Messages: 9
- Enregistré le: 27 Mai 2021, 12:15
-
 par John38 » 27 Mai 2021, 15:58
par John38 » 27 Mai 2021, 15:58
Je ne comprends pas pourquoi il faut s'intéresser à g(2) ou g(-2)
-
azf
 par azf » 27 Mai 2021, 16:02
par azf » 27 Mai 2021, 16:02
John38 a écrit:Je ne comprends pas pourquoi il faut s'intéresser à g(2) ou g(-2)
moi aussi je ne comprend pas l'utilité de tas de choses mais je les fait car c'est comme ça
Je repose mes quatre questions : que vaut g(2) ? et que vaut f(g(2))?
que vaut g(-2) ? et que vaut f(g(-2))?
Si vous auriez répondu à mes quatre questions au lieu de demander à quoi ça sert eh bien vous auriez fini
-
John38
- Messages: 9
- Enregistré le: 27 Mai 2021, 12:15
-
 par John38 » 27 Mai 2021, 16:22
par John38 » 27 Mai 2021, 16:22
-
azf
 par azf » 27 Mai 2021, 16:27
par azf » 27 Mai 2021, 16:27
 = \dfrac{1}{x-1})
et
\ =\ x^2-3)
\left(2\right)=f\left(g(2)\right)=\dfrac{1}{g(2)-1}=\dfrac{1}{2^2-3-1} =\dfrac{1}{4-3-1}=\dfrac{1}{4-4}=)
ça fait quoi au final?
-
azf
 par azf » 27 Mai 2021, 16:41
par azf » 27 Mai 2021, 16:41
John38 a écrit: = -7)
?????????? là je ne vois pas d'où sort le -7
^2-3=\left(\left(-2\right)\times \left(-2\right)\right)-3=\left(\left(-1\right)\left(-1\right)\times 2 \times 2\right) -3 =\left( 1\times 4\right)-3=4-3=1)
-
John38
- Messages: 9
- Enregistré le: 27 Mai 2021, 12:15
-
 par John38 » 27 Mai 2021, 16:48
par John38 » 27 Mai 2021, 16:48
Ce qui donne
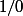
ce qui n'est pas possible. C'est une valeur interdite.
Cela voudrait dire que fog est défini sur ]-∞;2[U]2;+∞[ ?
-
azf
 par azf » 27 Mai 2021, 16:53
par azf » 27 Mai 2021, 16:53
John38 a écrit:Ce qui donne
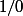
ce qui n'est pas possible. C'est une valeur interdite.
Cela voudrait dire que fog est défini sur ]-∞;2[U]2;+∞[ ?
non mais presque ...
que donne g(-2)?
-
mathelot
 par mathelot » 27 Mai 2021, 16:59
par mathelot » 27 Mai 2021, 16:59
une autre manière de faire, c'est se donner une indéterminée X (juste une lettre)
on fait les calculs avec X
=\dfrac{1}{X-1} et g(X)=X^2-3)
on calcule
(X) \,)
et
(X))
puis en revenant à la variable réelle

, on trouve les domaines de définition des
fonctions
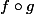
et
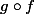
-
John38
- Messages: 9
- Enregistré le: 27 Mai 2021, 12:15
-
 par John38 » 27 Mai 2021, 17:02
par John38 » 27 Mai 2021, 17:02
g(-2) = 1
et g(2) est lui aussi égal à 1
fog serait alors défini sur ]-∞;1[U]1;+∞[ ?
-
azf
 par azf » 27 Mai 2021, 17:07
par azf » 27 Mai 2021, 17:07
John38 a écrit:g(-2) = 1
et g(2) est lui aussi égal à 1
fog serait alors défini sur ]-∞;1[U]1;+∞[ ?
Non Camarade
si vous prenez 2 ou si vous prenez -2 vous savez que g(2)=g(-2)=1 et vous savez que ça va donner une division par zéro
et que donc l'ensemble de définition de fog ne doit pas contenir 2 et -2
mais attention si on vous demande pourquoi ni 2 ni -2 ne sont pas dedans ne dites surtout pas qu'un certain punk alcoolique amateur de chimie toulousaine vous l'a soufflé car je suis nul en chimie et on a vu ce que ça donne un nul en chimie à Toulouse
2 et -2 sont les racines de x^2-4 et d'où vient ce polynôme? sinon de x^2-3 =1
et on sait qu'il ne faut pas qu'elle vaut 1 pour aller dans f
-
mathelot
 par mathelot » 27 Mai 2021, 17:14
par mathelot » 27 Mai 2021, 17:14
@azf: je te laisse avec @john38

-
John38
- Messages: 9
- Enregistré le: 27 Mai 2021, 12:15
-
 par John38 » 27 Mai 2021, 17:14
par John38 » 27 Mai 2021, 17:14
Donc ]-∞;-2[U]2;+∞[
-
azf
 par azf » 27 Mai 2021, 17:20
par azf » 27 Mai 2021, 17:20
mathelot a écrit:@azf: je te laisse avec @john38

Bonjour Mathelot et merci (j'espère qu'il va lire ce que tu as dit : c'est important car en plus moi je sais pas expliquer les choses comme un prof mais bon des fois je viens quand je vois que ça rame et que c'est de mon niveau (évidemment si c'est de mon niveau car sinon je coule au lieu de ramer et on va couler ensemble le demandeur et moi)
En fait on a fini il vient juste de terminer
Salut à plus les camarades John et Mathelot
-
John38
- Messages: 9
- Enregistré le: 27 Mai 2021, 12:15
-
 par John38 » 27 Mai 2021, 17:28
par John38 » 27 Mai 2021, 17:28
Merci beaucoup pour votre aide.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 27 Mai 2021, 17:32
par GaBuZoMeu » 27 Mai 2021, 17:32
Bonjour,
Fini, vraiment ?
La dernière réponse est incorrecte.
Il serait peut-être plus facile de l'écrire sous la forme

privé de ...
Modifié en dernier par
GaBuZoMeu le 27 Mai 2021, 17:33, modifié 1 fois.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités


