Bonjour, je suis en première année de prepa et je doit faire un exercice qui est de calculer la derivé n-ieme de la fonction f(x) = 1/(x^2-xcos(a) +1)
Je ne vois pas comment faire, j'ai essayer de calculer les première derive pour voir si il y avait une relation de récurrence mais je ne vois pas. De plus le binôme de Newton version derivé ne marche pas.
Avez-vous des suggestions pour m'aider ?
Derivé n-ième
8 messages
- Page 1 sur 1
Re: Derivé n-ième
bonjour,
on pose)
il vient+1)=1)
on peut appliquer la formule du binôme pour calculer la dérivée n-ième du produit.
Cette dérivée n-ième se résume à trois termes on obtient une formule de récurrence liant
},y^{(n-1)},y^{(n-2)})
on peut donc expliciter une formule de récurrence. Je ne sais si ça fait avancer les choses
on pose
il vient
on peut appliquer la formule du binôme pour calculer la dérivée n-ième du produit.
Cette dérivée n-ième se résume à trois termes on obtient une formule de récurrence liant
on peut donc expliciter une formule de récurrence. Je ne sais si ça fait avancer les choses
Re: Derivé n-ième
ah oui, ,j'ai la méthode ! :
on décompose+1}) en somme de deux éléments simples sur le corps des complexes et ensuite on peut dériver n fois les deux termes de la somme.
en somme de deux éléments simples sur le corps des complexes et ensuite on peut dériver n fois les deux termes de la somme.
remarque: on suppose que a est un réel
on décompose
remarque: on suppose que a est un réel
Modifié en dernier par mathelot le 06 Avr 2021, 18:31, modifié 1 fois.
Re: Derivé n-ième
Bonjour,
Autre idée, on peut écrire f( x) sous la forme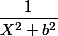
avec X=}2) et
et }4)
on fait une décomposition en éléments simples dans C
=\dfrac{i}{2} (\dfrac1{x+ib}-\dfrac1{x-ib}))
après on a dérivée nième de^n n!}{(x+\alpha)^{n+1)}}) et on l'applique.
et on l'applique.
Autre idée, on peut écrire f( x) sous la forme
avec X=
on fait une décomposition en éléments simples dans C
après on a dérivée nième de
Re: Derivé n-ième
phyelec a écrit:on fait une décomposition en éléments simples dans C
il y a une faute
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
