Combien de Solutions
5 messages
- Page 1 sur 1
Combien de Solutions
par MMu » 31 Mar 2021, 11:22
Soit 
un réel positif . Combien de solutions réelles positives a l'équation suivante :
+x=p\ln(p)+p)
Re: Combien de Solutions
par Rhaegar » 31 Mar 2021, 15:19
Bonjour,
x=p est solution. La fonction à gauche de l'égalité est strictement croissante donc cette solution est unique.
La réponse est donc une solution.
x=p est solution. La fonction à gauche de l'égalité est strictement croissante donc cette solution est unique.
La réponse est donc une solution.
Re: Combien de Solutions
par hdci » 31 Mar 2021, 15:54
La fonction à gauche n'est pas strictement croissante.
La dérivée est}{2}+\dfrac{p}{x})
Et pour p=0.001 on a\approx -0.8<0)
En fonction de p, elle est strictement croissante si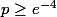
, ou bien croissante puis décroissante puis croissante (strictement s'entend)
La dérivée est
Et pour p=0.001 on a
En fonction de p, elle est strictement croissante si
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Combien de Solutions
par Rhaegar » 31 Mar 2021, 20:42
En effet. J'étais persuadé qu'un produit de fonctions croissantes était croissant 
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :