Limite de fonction

[LéaM1213]

Au pire donner moi la réponse directe, pour que je travail dessus. Avec la correction en général je comprend, et ensuite je m'entraine sur d'autre exercice similaire.

[LéaM1213]

Au pire donner moi la réponse directe, pour que je travail dessus. Avec la correction en général je comprend, et ensuite je m'entraine sur d'autre exercice similaire. Je vous assure que ça me convient mieux cette façon d'apprendre . Les élèves de ma classes ne veulent pas m'aider, je suis seul. J'ai pas d'amis, j'ai pas de famille. Je ferais tous ce que vous voulez en échange. Par pitié, aidez moi

[LéaM1213]

Bon j'ai compris, vous ne me répondrez plus. Il me reste plus qu'à mourir. Sérieux je vais avoir un zéro. Aidez moi s'il vous plait. Ayez un peu de pitié pour moi.

[LéaM1213]

Je ne vous demande pas de me faire une évaluation, je vous demande de m'aider à faire des exercices. Pitié

[LéaM1213]

Pitié aidez moi. Vous aurez mon échec scolaire sur votre conscience. Vous vous moquez de moi car je n'y arrive pas, mais moi je me moque de vous car vous faite rien pour m'aidez. Vous préférez juste m'ignorer en me laissant à mon triste sort.

[ijkl]

Personne ne se moque de toi Lea

Il faut laisser les gens le temps de répondre (tu sais moi par exemple mon chat vomi par terre et si je ne lave pas et prends ma serpillère je vais me casser la figure en glissant )

Je ne suis pas qualifié pour aider car bon je suis hors cursus mais bon de ce que j'ai compris tu dois enlever de l'ensemble des réels tous les x qui vont faire que dans une racine carrée la formule à l'intérieur sera négative

dans une fraction tu enlèvera tous les x qui feront que tu te trouvera avec une division par zéro

Mon chat vient de vomir dans la vaisselle que je vient de laver (il est si mignon que je commence à aimer faire la vaisselle

Ils viendront t'aider l'ami (laisse leur le temps de venir CAMARADE

[LéaM1213]

Merci, j'ai honte veillez me pardonner, j'ai un TDAH. Je monte sur mes grand chevaux pour un oui ou pour un non. Mais merci pour les indications.

[ijkl]

Je n'ai rien à pardonner (je ne suis qu'une machine -enfin j'essaye de l'être - et les machines n'ont pas ce pouvoir et ne l'auront jamais)

D'ailleurs j'ai souvent honte en maths (faut apprendre à vivre avec et on arrive à les aimer au final)

Bon courage à vous

[hdci]

Comme dit ijkl, il faut laisser le temps de répondre. Personnellement, ce n'est pas mon boulot (et je ne suis pas payé pour cela) d'être assis devant mon ordinateur pour répondre aux demandes des uns et des autres.
Mais je comprends que plus le temps avance plus la panique s'installe également.

Si je ne donne pas de but en blanc les réponses, c'est bien parce que cela n'aiderait pas. Sinon, tout le monde deviendrait médecin (il suffirait qu'on nous souffle les réponses à l'examen), mais perso j'aime bien savoir que mon médecin a passé un vrai examen avec de vraies difficultés et qu'il a réussi, et je n'aimerais pas monter dans un avion piloté par quelqu'un qui est devenu pilote parce que quelqu'un lui a soufflé les réponses sur un forum.

Pour revenir au problème : si vous n'avez pas les bases pour résoudre le problème, on peut vous aider à les retrouver, mais encore faut-il savoir les bases qui vous manquent.

1) Règle applicable aux polynômes du second degré : si et si et sont les deux racines distinctes du polynôme (cas du discriminant strictement positif), alors P(x) est du signe de a si...

Savez-vous répondre à cette question ? Si non, êtes vous allée voir dans votre cours (chapitre "second degré") ?


(Au passage : vous êtes en quelle classe ? Juste pour pouvoir adapter la réponse au bon niveau)

[LéaM1213]

...et seulement si et seulement si a est positif non?
Je suis en terminal.

[hdci]

...et seulement si et seulement si a est positif non?

Prenons pour l'exemple, les deux racines sont -1 et 1 (vous pouvez vérifier rapidement que P(-1)=0 et P(1)=0).

Ici le coefficient a qui multiplie le x au carré est égal à 1 donc est positif.

Pourtant,.

Donc ce n'est pas "si et seulement si a est positif".

Il faut donc bien reprendre les bases : si les racines sont et en considérant alors on peut factoriser le polynôme



Pour déterminer le signe, on fait un tableau de signes. Pour cela :

• en première ligne, on place les points particuliers de la droite numérique dans l'ordre : ici, moins l'infini, puis x1, puis x2, puis plus l'infini. Chaque point fait une séparation de colonne dans le tableau.
• En seconde ligne, on indique le signe de , sachant que on insicrit donc "+". Dans chaque case, selon qu'on soit avant ou après x1, on écrit le signe correspondant, en mettant 0 juste en-dessous de x1
• On fait pareil avec
• En dernière ligne, on applique la règle des signes : plus par plus et moins par moins, cela fait plus, sinon cela fait moins. Et comme le polynôme est a(x-x_1)(x-x_2), on n'oublie pas de considérer le signe de a.

Cela donne ce tableau (il faudrait ajouter les traits verticaux sous les infinis et sous les x1, x2 pour bien faire "tableau"

si



si



On en déduit que est du signe de "à l'extérieur des racines" soit dans

Vous êtes en terminale générale, spécialité maths ou STMG ?

[mathelot]

bonsoir,
l'écriture du domaine de définition de f est ici difficile ^^

on utilise la propriété
le trinôme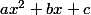 est du signe de à l'extérieur de l'intervalle des racines.
à apprendre par coeur.



il faut faire un tableau de signes des deux trinômes.

au final

[LéaM1213]

Merci pour tout je suis en spé math

[mathelot]

bonsoir,
l'écriture du domaine de définition de f est ici difficile ^^

on utilise la propriété
le trinôme est du signe de à l'extérieur de l'intervalle des racines.
à apprendre par coeur.



il faut faire un tableau de signes des deux trinômes.

au final, le domaine de définition de f, noté D(f) vaut:

Preuve:




Le domaine de définition D(f) s'écrit:


Il est de la forme où A,B,C,D sont des intervalles de R.

Il se trouve que l'intersection distribue sur la réunion,i.e :
(*)



(*) donne:





f admet une limite en tout point de
f admet une limite à gauche en x=-2 et f admet une limite à droite en x=2

En x=0, j'ai envie de dire que f n'admet pas de limite mais par contre est continue en x=0.

[LéaM1213]

Merci beaucoup et bonne année à vous, bonne santé surtout, et que cette nouvelle année soie mieux que la précédente. Vous m'avez réellement étais d'une grande aide.