Fonction limite d'une suite de fonction (DM de fou!)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Anonyme
 par Anonyme » 23 Oct 2013, 11:00
par Anonyme » 23 Oct 2013, 11:00
Bonjour, j'ai un exercice avec comme fonction : fn(x)= 1/(1+x^n)
Je n'ai jamais vu ce genre de fonction. Elle est définie sur R+.
Quelle est la variable n ou x? Comment l'étudier.
J'ai plusieurs questions
1) a. Déterminer, pour n > ou = 1, les variations de fn.
Comment faire la dérivée de cette fonction? J'ai pensé à fn'(x)= -1/(1+x^n)²
b. Démontrer que les courbes Cn passent toutes par deux points fixes que l'on déterminera.
J'ai absolument aucune idée de comment faire, à quoi ressemble cette fonction, je peux la rentrer dans ma calculette?
c. Soient deux entiers n et m non nuls avec nComparer fn(x) et fm(x) selon les valeurs de x.
En déduire les positions relatives de Cn et Cm.
Faut-il faire varier aussi le n et le m ou uniquement le x?
Pour la suite j'essaierai de me débrouiller. :mur:
Merci d'avance et bonne journée.
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 23 Oct 2013, 11:06
par mcar0nd » 23 Oct 2013, 11:06
Miaouwrion a écrit:Bonjour, j'ai un exercice avec comme fonction : fn(x)= 1/(1+x^n)
Je n'ai jamais vu ce genre de fonction. Elle est définie sur R+.
Quelle est la variable n ou x? Comment l'étudier.
J'ai plusieurs questions
1) a. Déterminer, pour n > ou = 1, les variations de fn.
Comment faire la dérivée de cette fonction? J'ai pensé à fn'(x)= -1/(1+x^n)²
b. Démontrer que les courbes Cn passent toutes par deux points fixes que l'on déterminera.
J'ai absolument aucune idée de comment faire, à quoi ressemble cette fonction, je peux la rentrer dans ma calculette?
c. Soient deux entiers n et m non nuls avec n<m
Comparer fn(x) et fm(x) selon les valeurs de x.
En déduire les positions relatives de Cn et Cm.
Faut-il faire varier aussi le n et le m ou uniquement le x?
Pour la suite j'essaierai de me débrouiller. :mur:
Merci d'avance et bonne journée.
Salut,la variable de ta fonction c'est x.

Alors ta fonction est de la forme
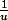
où
=1+x^n)
. Quelle est la dérivée d'une fonction de cette forme?
-
Anonyme
 par Anonyme » 23 Oct 2013, 11:12
par Anonyme » 23 Oct 2013, 11:12
ça serait -u'/u² donc -(nx^n-1)/(1+x^n)² ?
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 23 Oct 2013, 11:17
par mcar0nd » 23 Oct 2013, 11:17
Miaouwrion a écrit:ça serait -u'/u² donc -(nx^n-1)/(1+x^n)² ?
Exactement, tu as ta dérivée.
Maintenant, il te faut le signe de f'(x). Pour ça, à mon avis, il faut que tu distingue 2 cas : n pair et n impair.
Commence lorsque n est pair, c'est un peu plus simple. LE signe de
^2)
c'est simple. Ensuite, celui de n tu le connais.
Et celui de
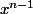
? Est ce que tu as une idée?

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 23 Oct 2013, 11:19
par chombier » 23 Oct 2013, 11:19
Miaouwrion a écrit:ça serait -u'/u² donc -(nx^n-1)/(1+x^n)² ?
C'est ça. En fait tu as une famille de fonctions :
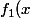=\frac{1}{1+x^1}=\frac{1}{1+x})
=\frac{1}{1+x^2})
=\frac{1}{1+x^3})
etc.
-
Anonyme
 par Anonyme » 23 Oct 2013, 11:28
par Anonyme » 23 Oct 2013, 11:28
(1+x^n)² > 0
Pourquoi distinguer deux cas?
n est un entier naturel.
x^n-1 > 0 tant que n>= 1
La dérivé est négative à cause du - au dénominateur donc la fonction fn est décroissante, c'est ça?
(Merci beaucoup de vos réponses)

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 23 Oct 2013, 11:33
par chombier » 23 Oct 2013, 11:33
Miaouwrion a écrit:(1+x^n)² > 0
Pourquoi distinguer deux cas?
n est un entier naturel.
x^n-1 > 0 tant que n>= 1
La dérivé est négative à cause du - au dénominateur donc la fonction fn est décroissante, c'est ça?
(Merci beaucoup de vos réponses)
Il faudrait distinguer deux cas si f_n était définie sur |R.
Comme elle est définie sur |R+, en effet, tu n'en as pas besoin
(1+x^n)² > 0 --> OK
x^n-1 > 0 tant que n>= 1 ---> NON
si x = 1/2, n = 1, (x^n-1) = (1/2-1) = -1/2
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 23 Oct 2013, 12:00
par mcar0nd » 23 Oct 2013, 12:00
Ah oui, j'avais pas fait attention que la fonction f était définie sur R+. :mur:
Pas besoin de distinguer deux cas alors. Merci chombier d'avoir corrigé mon erreur. ;)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
