Limite de fonction
35 messages
- Page 1 sur 2 - 1, 2
Limite de fonction
Bonjour, j'ai une évaluation à la rentrée donc pour m'entrainer j'ai décidé de piocher au hasard dans mon manuel de math, et je reste bloqué sur un exercice. Pouvez m'aider!
j'ai un vrai problème avec les consignes, je sais faire les choses, mais je ne sais pas vraiment quand les faires. Je ne sais pas si cela était claire, mais bref, voila le sujet.
En quels points, peut-on étudier la limite de la fonction f (x)= √ x( x−2)−√ x(x+2) ?
J'ai vraiment du mal, pourtant je suis sûre que c'est un truc tout bête. Voila, merci d'avance.
j'ai un vrai problème avec les consignes, je sais faire les choses, mais je ne sais pas vraiment quand les faires. Je ne sais pas si cela était claire, mais bref, voila le sujet.
En quels points, peut-on étudier la limite de la fonction f (x)= √ x( x−2)−√ x(x+2) ?
J'ai vraiment du mal, pourtant je suis sûre que c'est un truc tout bête. Voila, merci d'avance.
Re: Limite de fonction
Bonjour,
Est-ce
-\sqrt{x}(x+2)) ou bien
ou bien }-\sqrt{x(x+2)}) ?
?
Comme vous n'avez pas mis de parenthèse, c'est donc la première version...
Quoi qu'il en soit, quand est-ce qu'on a le droit de calculer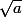 (pour quels nombres
(pour quels nombres  cette expression a-t-elle du sens) ?
cette expression a-t-elle du sens) ?
Est-ce
Comme vous n'avez pas mis de parenthèse, c'est donc la première version...
Quoi qu'il en soit, quand est-ce qu'on a le droit de calculer
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Limite de fonction
Bonjour et merci de m'avoir répondu.
Donc c'est le deuxième cas.
Je ne comprend pas vraiment mais je vous ai donné l'exercice en entier, il n'y a rien d'autre.
Donc c'est le deuxième cas.
Je ne comprend pas vraiment mais je vous ai donné l'exercice en entier, il n'y a rien d'autre.
Re: Limite de fonction
Donc si j'ai bien compris il, faut calculer le domaine de définition :
Ce qui donne R/ }-2} car quand x=-2 , la fonction =0.
Merci mais ça n'est pas tous?
Ce qui donne R/ }-2} car quand x=-2 , la fonction =0.
Merci mais ça n'est pas tous?
Re: Limite de fonction
Bonjour,
Effectivement, il faut d'abord déterminer le domaine de définition, puisqu'on ne peut calculer les limites qu'en des nombres du domaine de définition, ou aux bornes du domaine de définition
(en effet, on détermine les limites "quand x s'approche de la cible", si la cible est carrément à l'extérieur du domaine de définition on ne peut pas s'en approcher).
Revenons à votre domaine de définition, vous avez écrit
J'ai du mal à comprendre car les notations sont fortement incorrectes, mais la fin ("quand x=-2 (...)") n'est pas le bon argument.
Quand on a des racines carrées, qu'est-ce qu'il faut vérifier ?
Effectivement, il faut d'abord déterminer le domaine de définition, puisqu'on ne peut calculer les limites qu'en des nombres du domaine de définition, ou aux bornes du domaine de définition
(en effet, on détermine les limites "quand x s'approche de la cible", si la cible est carrément à l'extérieur du domaine de définition on ne peut pas s'en approcher).
Revenons à votre domaine de définition, vous avez écrit
LéaM1213 a écrit:Ce qui donne R/ }-2} car quand x=-2 , la fonction =0.
J'ai du mal à comprendre car les notations sont fortement incorrectes, mais la fin ("quand x=-2 (...)") n'est pas le bon argument.
Quand on a des racines carrées, qu'est-ce qu'il faut vérifier ?
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Limite de fonction
AH oui, j'ai confondu avec les fractions ou il faut vérifier que le résutat n'est pas egal à 0. Donc ici il faut vérifier que le nombre sous la racine n'est pas négatif.
Ainsi (rc(...) pour dire racine de... :
Soit x appartient à R f(x) existe si et seulement si:
rc (x(x-2))-rc (x(x+2) )>0
Je bloque à ce niveau.
Ainsi (rc(...) pour dire racine de... :
Soit x appartient à R f(x) existe si et seulement si:
rc (x(x-2))-rc (x(x+2) )>0
Je bloque à ce niveau.
Re: Limite de fonction
Attention, ce n'est pas f(x) qui doit être positif, mais ce qu'il y a sous les racines.
Par exemple : si x=1, peut-on calculer ?
Mais si x=2, quel est le signe de f(x) ? Pourtant vous l'avez bien calculé...
Il faut étudier le signe de) et celui de
et celui de ) et le domaine de définition est l'ensemble (réunion d'intervalles très certainement) pour lequel ces deux polynômes sont simultanément positifs.
et le domaine de définition est l'ensemble (réunion d'intervalles très certainement) pour lequel ces deux polynômes sont simultanément positifs.
Comment fait-on pour étudier le signe d'un polynôme ? Deux méthodes possibles ici ; vous avez certainement vu le signe des polynômes de la forme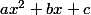
Par exemple : si x=1, peut-on calculer ?
Mais si x=2, quel est le signe de f(x) ? Pourtant vous l'avez bien calculé...
Il faut étudier le signe de
Comment fait-on pour étudier le signe d'un polynôme ? Deux méthodes possibles ici ; vous avez certainement vu le signe des polynômes de la forme
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Limite de fonction
Pour étudier le signe d'un polynôme on commence par trouver les racine:
Pour x(x-2) la racine est 2
Pour x(x+2) la racine est -2
Pour x(x-2) la racine est 2
Pour x(x+2) la racine est -2
Re: Limite de fonction
Dans un polynôme du second degré, souvent il y a deux racines...
Quand le polynôme est factorisé, on lit directement les racines...
Quand le polynôme est factorisé, on lit directement les racines...
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Limite de fonction
Bonjour et excusez-moi s'il vous plait, j'ai rencontré des problème hier soir, et j'ai dû arrêter mais devoirs. Cela ne se reproduira plus.
Donc les racines sont:
Pour x(x-2) les racines sont 2 et 0
Pour x(x+2) les racines sont -2 et 0.
Donc les racines sont:
Pour x(x-2) les racines sont 2 et 0
Pour x(x+2) les racines sont -2 et 0.
Re: Limite de fonction
écris l'ensemble de définition de f comme réunion d'intervalles et d'un singleton
Re: Limite de fonction
Excusez-moi mais je n'est jamais entendu le terme "singleton" donc je ne comprend pas ce que vous me demandez.
Re: Limite de fonction
Pouvez vous m'aiguiller sur ce que je doit faire en détaille. Pour que je comprenne mieux. Ce forum est un des nombreux forum que j'ai consulté, et je trouve que vous restez trop vaste dans vos réponse. Bien évidement je suis consciente que c'est de ma faute, puisque je suis vraiment pas doué. Mais s'il vous plaît pouvez-vous prendre en compte mais nombreuse lacunes et difficultés. Merci bien.
Re: Limite de fonction
un singleton est un ensemble à un élément. par exemple  est l'ensemble contenant le nombre zéro
est l'ensemble contenant le nombre zéro
l'usage serait d'écrire l'intervalle [0] plutôt
l'usage serait d'écrire l'intervalle [0] plutôt
Re: Limite de fonction
N'écrivez pas les intervalles "au hasard au petit bonheur la chance" : soit vous connaissez la règle de signe du polynôme du second degré, soit vous faites un tableau de signe.
Dans quel cas le polynôme x(x-2) est-il positif ?
1) Règle applicable aux polynômes du second degré : si=ax**2+bx+c) et si
et si  et
et sont les deux racines distinctes du polynôme (cas du discriminant strictement positif), alors P(x) est du singe de a si... ?
sont les deux racines distinctes du polynôme (cas du discriminant strictement positif), alors P(x) est du singe de a si... ?
2) Si vous ne connaissez pas cette règle (mais ce serait surprenant : un exercice avec des limites, vous êtes au moins en première donc vous avez forcément cela dans votre cours), vous faites un tableau de signes.
C'est parce que la seule façon de progresser, c'est de faire le travail de recherche. L'effort que vous aurez fait pour comprendre comment cela marche restera gravé dans votre cerveau et vous serez capable de le refaire sans aide.
Dans quel cas le polynôme x(x-2) est-il positif ?
1) Règle applicable aux polynômes du second degré : si
2) Si vous ne connaissez pas cette règle (mais ce serait surprenant : un exercice avec des limites, vous êtes au moins en première donc vous avez forcément cela dans votre cours), vous faites un tableau de signes.
LéaM1213 a écrit:Ce forum est un des nombreux forum que j'ai consulté, et je trouve que vous restez trop vaste dans vos réponse.
C'est parce que la seule façon de progresser, c'est de faire le travail de recherche. L'effort que vous aurez fait pour comprendre comment cela marche restera gravé dans votre cerveau et vous serez capable de le refaire sans aide.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Limite de fonction
Désolé mais je ne comprend vraiment rien. Oui c'est surprenant d'être aussi conne. Mais je fait du mieux que je peux. Ma famille ont de gros problème financier de ce faite j'ai était harcelé. J'ai décidé de ne plus allé en cour, et j'ai extrêmement besoin d'aide, j'ai fait une grosse erreur et je le regrette alors, s'il vous plait ce forum c'est tout ce qu'il me reste, que fait-il que je face clairement ?
Re: Limite de fonction
S'il vous plaît aidez moi ! Je ne sais pas quoi faire. Mon évaluation est le lundi de la rentrée. J'ai besoin de m'entraîner sur ce type d'exercice, qui tombera probablement. Je vous en supplie c'est trop important, ne m'abandonné pas. J'ai peur.
35 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
