Bonsoir les matheux ..
une petite question sur les fonctions intègrables au sens de Riemann .. je veux montrer que la fonction -pour tout n naturel-

par
= \int_{0}^{1} \frac{1}{(x+t^2)^n}\, dt)
est intègrable .. je veux appliquer le critère d'intègrablité au sens de Riemann ..
Est ce que vous pourrez m'aider à prouver ceci s'il vous plaît ?
merci bien d'avance ...
Rappel d'une fonction intègrable au sens de Riemann:
la fonction

une fonction bornée est intègrable au sens de Riemann si

avec
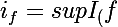)
et

c'est l'ensemble des fonction en escalier qui minorent
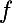
et
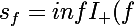)
et

c'est l'ensemble des fonctions en escalier qui majorent f et la borne commune c'est l'intègrale de
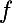
.
et de là on en déduit le critère d'intègrabilité

bornée est intègrable au sens de Riemann ssi pour tout

il existe
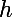
fonction en escalier qui minorent
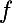
et
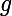
fonction en escalier qui majorent
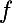
tel que

..
