Bonjour j'ai du mal a montrer une implication
Montrer que
g(f) injective
f surjective
Implique
g injective
Merci
Fonction surjective /injective
4 messages
- Page 1 sur 1
Re: Fonction surjective /injective
Par g(f), tu désignes la composée 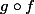 , n'est-ce pas.
, n'est-ce pas.
Qu'as-tu essayé ?
Dans une situation abstraite comme celle-ci, le seul outil à notre disposition est de revenir aux définitions.
Fixons les notations :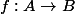 et
et 
Que veut dire " injective". Ça veut dire que pour tous
injective". Ça veut dire que pour tous  dans
dans  , si
, si =g(y)) , alors
, alors  . C'est ça qu'il faut démontrer, en utilisant les hypothèses :
. C'est ça qu'il faut démontrer, en utilisant les hypothèses : 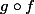 injective et
injective et  surjective.
surjective.
Qu'as-tu essayé ?
Dans une situation abstraite comme celle-ci, le seul outil à notre disposition est de revenir aux définitions.
Fixons les notations :
Que veut dire "
Re: Fonction surjective /injective
Comme g(f) injective alors g(f(x)) =g(f(x')) implique que f(x)= f(x')
Et comme f surjective les images admettent au moins un antécédents par f
Et comme f surjective les images admettent au moins un antécédents par f
Re: Fonction surjective /injective
Je dirais plutôt que puisque 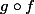 est injective, pour tous
est injective, pour tous 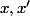 de
de  , si
, si )=g(f(x'))) alors
alors 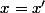 (et par conséquent
(et par conséquent =f(x')) .
.
Une imùage admet toujours un antécédent, par définition de l'image. Tu n'écris peut-être pas ce que tu voudrais écrire.
Je te rappelle : pour démontrer que est injective, on part de deux éléments (tu peux les appeler
est injective, on part de deux éléments (tu peux les appeler  et
et 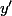 si ça te chante) de
si ça te chante) de  et on suppose que
et on suppose que =g(y')) . On veut montrer que
. On veut montrer que 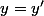 .
.
Et comme f surjective les images admettent au moins un antécédents par f
Une imùage admet toujours un antécédent, par définition de l'image. Tu n'écris peut-être pas ce que tu voudrais écrire.
Je te rappelle : pour démontrer que
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
