Produits de deux fonctions intègrable !
26 messages
- Page 1 sur 2 - 1, 2
Produits de deux fonctions intègrable !
Salut tout le monde ..
(tiens ça fais un moment !! )
vous manquez .. lol ..
Donc j'ai un petit soucie ..
Je souhaite montrer que le produit de f :[a,b]->R intègrable au sens de Riemann et g:[a,b]->R intègrable au sens de Riemann aussi .. est une fonction intègrable au sens de Riemann .. par la méthode la plus astucieuse possible ..
Pourriez vous m'aider donc ?
Merci d'avance ..
(tiens ça fais un moment !! )
vous manquez .. lol ..
Donc j'ai un petit soucie ..
Je souhaite montrer que le produit de f :[a,b]->R intègrable au sens de Riemann et g:[a,b]->R intègrable au sens de Riemann aussi .. est une fonction intègrable au sens de Riemann .. par la méthode la plus astucieuse possible ..
Pourriez vous m'aider donc ?
Merci d'avance ..
Salut ..
si tu veux la vraie définition est bien la suivante :
la fonction f:[a,b]->R une fonction bornée est intègrable au sens de Riemann si avec
avec  =sup I_(f) et I_ c'est l'ensemble des fonction en escalier qui minorent f et
=sup I_(f) et I_ c'est l'ensemble des fonction en escalier qui minorent f et  = inf I+(f) et I+ c'est l'ensemble des fonctions en escalier qui majorent f et la borne commune c'est l'intègrale de f .
= inf I+(f) et I+ c'est l'ensemble des fonctions en escalier qui majorent f et la borne commune c'est l'intègrale de f .
et de là on en déduit le critère d'intègrabilité f:[a,b]->R bornée est intègrable au sens de Riemann ssi pour tout epsilon > 0 il existe h fonction en escalier qui minorent f et g fonction en escalier qui majorent f tq intégrale entre a et b g-h < epsilon ..
si tu veux la vraie définition est bien la suivante :
la fonction f:[a,b]->R une fonction bornée est intègrable au sens de Riemann si
et de là on en déduit le critère d'intègrabilité f:[a,b]->R bornée est intègrable au sens de Riemann ssi pour tout epsilon > 0 il existe h fonction en escalier qui minorent f et g fonction en escalier qui majorent f tq intégrale entre a et b g-h < epsilon ..
[quote="sandrine_guillerme"]f:[a,b]->R bornée est intègrable au sens de Riemann ssi pour tout epsilon > 0 il existe h fonction en escalier qui minorent f et g fonction en escalier qui majorent f tq intégrale entre a et b g-h 0[/TEX]
il existe h fonction en escalier qui minorent f et k fonction en escalier qui majorent f+sup(h+h')|+1})
il existe h' fonction en escalier qui minorent g et k' fonction en escalier qui majorent g+sup(h+h')|+1})
donc hh' fonction en escalier qui minorent fg et kk' fonction en escalier qui majorent fg
et on a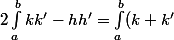(k'-h')+(h+h)'(k-h)<(|sup(k+k')+sup(h+h')|+1)(\int_{a}^{b}k-h+k'-h')<a)
sauf erreur
si j'ai fait une faute, c'est tres normal car la notion d'intergrabilité au sens de Riemann est nouveau pour moi
il existe h fonction en escalier qui minorent f et k fonction en escalier qui majorent f
il existe h' fonction en escalier qui minorent g et k' fonction en escalier qui majorent g
donc hh' fonction en escalier qui minorent fg et kk' fonction en escalier qui majorent fg
et on a
sauf erreur
si j'ai fait une faute, c'est tres normal car la notion d'intergrabilité au sens de Riemann est nouveau pour moi
mais je t'en prie aviateurpilot !!! c'est sympa de m'aider ..
Yipee , oula!! tu m'a fais un peu de doute .. regarde cet exemple
surlequel c'est assez dur de voir ce que tu viens de me dire ..
Yipee , oula!! tu m'a fais un peu de doute .. regarde cet exemple
surlequel c'est assez dur de voir ce que tu viens de me dire ..
aviateurpilot a écrit:je viens de savooir c'est quoi intègrable au sens de Riemann
si j'ai bien compris voila ma solution:
soit
il existe h fonction en escalier qui minorent f et k fonction en escalier qui majorent f
il existe h' fonction en escalier qui minorent g et k' fonction en escalier qui majorent g
donc hh' fonction en escalier qui minorent fg et kk' fonction en escalier qui majorent fg
et on a
sauf erreur
si j'ai fait une faute, c'est tres normal car la notion d'intergrabilité au sens de Riemann est nouveau pour moi
Tu n'as pas considéré que les fonctions ne sont pas forcement positives.
sandrine_guillerme a écrit:mais je t'en prie aviateurpilot !!! c'est sympa de m'aider ..
Yipee , oula!! tu m'a fais un peu de doute .. regarde cet exemple
surlequel c'est assez dur de voir ce que tu viens de me dire ..
tu peux regarder ma solution si j'ai pas fait une betise dans ce exemple
http://maths-forum.com/showthread.php?t=22060&highlight=continuit%E9
dans ce exemple le nombre de point de discontinuité n'est pas négligable
car si j'ai bien compris cette notion (negliger ...) n'ai pas negligable devant
n'ai pas negligable devant 
mais pour ce exemple
=0)

=1)
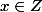
le nombre de point de discontinuité est négligable
car si j'ai bien compris cette notion (negliger ...)
mais pour ce exemple
le nombre de point de discontinuité est négligable
si A et B sont deux ensemble (A inclus dans B), quand, on peux dire que A est negligable devant B ?? :hein:
26 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
