Bonjour Je m'identifie au pseudo HAITITOUTAN
Je suis en train de faire un exercice de math mais Je ne peut pas le faire
Voila l'exercice.
Determiner l'ensemble des nombres complexes Z appartient C privée de 0 tels que Z^7 et 1/Z^2 soient conjugués.
Je suis en debutant à l'enseignement superieur
Si quelqu'un pourrait le faire aide-moi ce serait très gentil.
Merci d'avance.
Equation sur les nombres complexe.
6 messages
- Page 1 sur 1
Re: Equation sur les nombres complexe.
Bonjour,
on peut passer en coordonnées polaires et poser
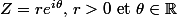
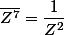
que devient l'équation quand Z est écrit sous forme trigonométrique ?
on peut passer en coordonnées polaires et poser
que devient l'équation quand Z est écrit sous forme trigonométrique ?
Re: Equation sur les nombres complexe.
HAITITOUTAN a écrit:Si quelqu'un pouvait le faire, aidez-moi ce serait très gentil.
Merci d'avance.
on pose l'équation
la conjugaison permute avec l'addition et la multiplication:
On pose
le conjugué de
en passant au conjugué
que peut on en déduire de cette dernière égalité ?
Re: Equation sur les nombres complexe.
mathelot a écrit:
que peut on en déduire de cette dernière égalité ?
on en déduit :
r=1
soient les racines cinquièmes de l'unité.
Les solutions de l'équation sont les racines cinquièmes de l'unité.
Modifié en dernier par mathelot le 26 Déc 2019, 17:43, modifié 1 fois.
Re: Equation sur les nombres complexe.
est-ce que la formule d'Euler est connue
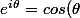+i sin(\theta)) pour
pour  réel
réel
?
On peut résoudre cette équation sans cette formule mais c'est nettement plus galère.
?
On peut résoudre cette équation sans cette formule mais c'est nettement plus galère.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
