Trigo 1ère - Formule de duplication et d'add.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Furi0u5
- Membre Relatif
- Messages: 449
- Enregistré le: 15 Oct 2005, 16:44
-
par Furi0u5 » 20 Nov 2006, 21:16
Bonsoir !
J'ai un petit exercice à faire pour mercredi mais... j'arrive pas utiliser les formulres de trigo correctement.
Il s'agit de démontrer l'égalité pour tout nombre x suivante:
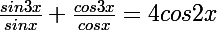
Alors avec ça je fais quoi?
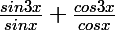
donne
}{sin x} + \frac {cos (2x + 1)}{cos x})
?
Après je vois pas comment faire :/
Peut-on dire que
}{sin x} =\Large\Large \frac{2x + 1}{x})
?
Merci!
-
pléon
- Membre Naturel
- Messages: 24
- Enregistré le: 11 Nov 2006, 15:40
-
par pléon » 20 Nov 2006, 21:19
Met les fractions au même dénominateur puis reconnaît les formules de cos(a+b) et sin(a+b) :we:
-
Furi0u5
- Membre Relatif
- Messages: 449
- Enregistré le: 15 Oct 2005, 16:44
-
par Furi0u5 » 20 Nov 2006, 21:23
Merci
=
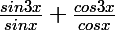
 + sin x \times cos (2x + 1)}{sin x \times cos x})
C'est toujours juste ça?
Merci
-
Furi0u5
- Membre Relatif
- Messages: 449
- Enregistré le: 15 Oct 2005, 16:44
-
par Furi0u5 » 20 Nov 2006, 22:10
Je me permet de upper, car j'aimerais le finir ce soir :zen:
Merci d'avance
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
par sue » 21 Nov 2006, 01:56
bon tu mélange les choses là : t'es sur que 2x+1 =3x ?!!!
d'abord tu as :
-
 = sin(2x+x) = sin(2x)cos(x) + sin(x)cos(2x))
-
= cos(2x+x)= cos(2x)cos(x) - sin(2x)sin(x))
donc :
}{sin(x)} = \frac{sin(2x)cos(x) + sin(x)cos(2x)}{sin(x)} = \frac{sin(2x)cos(x)}{sin(x)} + \frac{sin(x)cos(2x)}{sin(x)} = \frac{sin(2x)cos(x)}{sin(x)} + cos(2x))
idem on a :
}{cos(x)} = \frac{cos(2x)cos(x)}{cos(x)} - \frac{sin(2x)sin(x)}{cos(x)} = cos(2x) - \frac{sin(2x)sin(x)}{cos(x)}...)
alors en sommant et en appliquant deux autres formules que tu connais surement , tu devrais t'en sortir :we:
-
Furi0u5
- Membre Relatif
- Messages: 449
- Enregistré le: 15 Oct 2005, 16:44
-
par Furi0u5 » 21 Nov 2006, 19:55
Merci beaucoup! :we:
bon tu mélange les choses là : t'es sur que 2x+1 =3x ?!!!
Ah oui mince !
Ouais donc 3x = 2x + x
J'arrive à ceci, et j'ai besoin de justifier ça, j'espère que c'est bon. Sinon je doit revenir en arrière?
 + cos (2x)} { sinx cos x})
= 2 cos 2x
Merci !!
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
par sue » 21 Nov 2006, 21:26
bon bon on est arrivé jusqu'à :
}{\sin(x)} + \frac{\cos(3x)}{\cos(x)} = 2cos(2x) + \frac{\sin(2x) \cos(x)}{\sin(x)} - \frac{\sin(2x)\sin(x)}{\cos(x)} = 2\cos(2x) + \frac{\sin(2x) (\cos^2(x) - \sin^2(x))}{\sin(x)\cos(x)} = ...)
reste à montrer mnt que
 (\cos^2(x) - \sin^2(x))}{\sin(x)\cos(x)} = 2cos(x))
à quoi égale
)
? par quoi peut-on remplacer
 - \sin^2(x))
?
en répondant tu devrais conclure :we:
-
Furi0u5
- Membre Relatif
- Messages: 449
- Enregistré le: 15 Oct 2005, 16:44
-
par Furi0u5 » 21 Nov 2006, 21:41
hmm..j'étais arrivé à:
2 cos (2x) +
 + cos (2x)}{sinx \times cosx})
= 4 cos2x
Mais apparament c'est faux
Alors:
pas = 2cos(x) mais = 2cos(2x)
}{sin(x)cos(x)} = 2cos(2x))
Voilà parfait :we: Suffit d'assembler les gros morceaux ! :zen:
Merci encore de l'aide!
Ps: sin(2x) sin²x = sin²(x) ?
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
par sue » 21 Nov 2006, 22:06
Ps: sin(2x) sin²x = sin²(x) ?
c FAUX !! d'ou vient ça ? t'es sur que t'as bien appris tes forumules de trigo ?!
voilà tt :
sin(2x) = 2sin(x) cos(x)
cos²(x) - sin²(x) = cos(2x)
-
Furi0u5
- Membre Relatif
- Messages: 449
- Enregistré le: 15 Oct 2005, 16:44
-
par Furi0u5 » 21 Nov 2006, 22:17
sue a écrit:c FAUX !! d'ou vient ça ? t'es sur que t'as bien appris tes forumules de trigo ?!
voilà tt :
sin(2x) = 2sin(x) cos(x)
cos²(x) - sin²(x) = cos(2x)
Non c'est rien en fait
Une petite erreur de calcul qui m'a ramené à ça^^
Et pour les formules de trigo je les ai sous les yeux donc c'est pas parceque je les ai pas apprises lol. Non mais je vais les apprendre maintenant :zen:
Vala problème résolu ! :id: Merci beaucoup Sue !
Bonne soirée, à+
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 102 invités
