Exercice sur les ensembles
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 29 Sep 2019, 14:47
par akiwhite » 29 Sep 2019, 14:47
Bonjour,
Je bloque sur deux petites questions qui ne sont surement pas difficiles, veuillez pardonner mon niveau déplorable en maths ^^ :
-1) Montrer que AΔB = BΔA, puis que (AΔB)ΔC = AΔ(BΔC) avec Δ la différence symetrique dans P(E)
-2)Montrer que A∩(BΔC) = (A∩B)Δ(B∩C)
1) Bon AΔB = BΔA c'est fait en développant et utilisant la commutativité, ensuite ben ... Je rame
2)En développant je ne trouve rien ..
Merci pour votre aide

-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 29 Sep 2019, 15:16
par GaBuZoMeu » 29 Sep 2019, 15:16
Si tu savais associer à une partie de

sa fonction caractéristique

, ça roulerait tout seul (la différence symétrique correspond à l'addition des fonctions caractéristiques, l'intersection au produit). Mais je suppose que tu n'as pas encore vu ça.
Un moyen de faire est alors de se ramener à des formes normales disjonctives (réunion d'intersections de parties ou de leurs complémentaires). Par exemple :
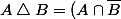\cup (\overline A \cap B))
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 29 Sep 2019, 15:53
par akiwhite » 29 Sep 2019, 15:53
Merci pour ta réponse mais en développant, les calculs deviennent immenses et je tombe dans un cul de sac !
Faut-il s'y prendre autrement ?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 29 Sep 2019, 16:51
par GaBuZoMeu » 29 Sep 2019, 16:51
Persévère. Tu te décourages trop facilement.
Même pour moi qui ne suis pas un fan des calculs, ils ne sont pas si pénibles. À moins que tu t'y prennes vraiment mal. Montre-nous ce que tu as tenté.
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 29 Sep 2019, 17:51
par akiwhite » 29 Sep 2019, 17:51
En développant :
J'obtiens (AΔB)ΔC = (((B ∩ nC) U (nB ∩ C)) ∩ nA) U (((B U nC) ∩ (nB U C) ∩ A) avec nA=nonA ...
et AΔ(BΔC) = (((A ∩ nB) U (nA ∩ B)) ∩ nC) U (((A U nB) ∩ (nA U B) ∩ C)
Désolé je ne sais pas comment présenter ca sans être illisible
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 29 Sep 2019, 17:57
par akiwhite » 29 Sep 2019, 17:57
Ensuite je peux aller plus loin en ditribuant ...
(AΔB)ΔC = (((B ∩ nC) U (nB ∩ C)) ∩ nA) U (((B U nC) ∩ (nB U C) ∩ A)
= ((nA ∩ B ∩ nC) U (nA ∩ nB ∩ C)) U (((A ∩ (B U nC)) ∩ ((A ∩ (nB U C)))
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 29 Sep 2019, 22:09
par GaBuZoMeu » 29 Sep 2019, 22:09
Ça ressemble plutôt à
)
, ce que tu calcules, non ? Et pourquoi t'arrêtes-tu en chemin ?

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 30 Sep 2019, 16:21
par fatal_error » 30 Sep 2019, 16:21
bj,
pour la une,
via table logique
En remarquant que la diff symétrique est le xor (je le représente par X)
- Code: Tout sélectionner
A|B|C|AXB|BXC|(AXB)XC|AX(BXC)
0|0|0| 0| 0| 0| 0
0|0|1| 0| 1| 1| 1
0|1|0| 1| 1| 1| 1
0|1|1| 1| 0| 0| 0
1|0|0| 1| 0| 1| 1
1|0|1| 1| 1| 0| 0
1|1|0| 0| 1| 0| 0
1|1|1| 0| 0| 1| 1
et on a bien les même lignes pour (AXB)XC et AX(BXC)
pour la 2), j'ai l'impression que l'égalité A∩(BΔC) = (A∩B)Δ(B∩C) est fausse:
- Code: Tout sélectionner
A|B|C|BXC|A(BXC)|AB|BC|(AB)X(BC)
0|0|0| 0| 0| 0| 0| 0
0|0|1| 1| 0| 0| 0| 0
0|1|0| 1| 0| 0| 0| 0
0|1|1| 0| 0| 0| 1| 0
1|0|0| 0| 0| 0| 0| 0
1|0|1| 1| 1| 0| 0| 0
1|1|0| 1| 1| 1| 0| 0
1|1|1| 0| 0| 1| 1| 1
A(BXC) et (AB)X(BC) n'ont pas les même lignes
la vie est une fête

-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 30 Sep 2019, 16:53
par GaBuZoMeu » 30 Sep 2019, 16:53
Il y a en fait une coquille dans la recopie de l'énoncé. L'égalité correcte est
 = (A\cap B)\bigtriangleup(A\cap C))
(un cas particulier de la distributivité de la multiplication par rapport à l'addition).
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 30 Sep 2019, 17:11
par akiwhite » 30 Sep 2019, 17:11
Effectivement je me suis trompé en recopiant la question 2 ...
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 30 Sep 2019, 17:15
par akiwhite » 30 Sep 2019, 17:15
GaBuZoMeu a écrit:Ça ressemble plutôt à
)
, ce que tu calcules, non ? Et pourquoi t'arrêtes-tu en chemin ?
Je ne trouve aucun lien entre les deux,
Et je ne sais pas comment continuer à développer !

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 30 Sep 2019, 17:32
par fatal_error » 30 Sep 2019, 17:32
wiki donne la def:
https://en.wikipedia.org/wiki/Exclusive_ormais je pense que ce qui est attendu est que tu te paluches la manipulation des U et ∩ en développant.
au pire du pire, je pense que tu peux simplifier les deux membres de l'égalité en somme de facteurs (genre F_1 UF_2 U F_3...) avec F_i que des "produits" d'intersections, etc, puis tu compares les deux formes simplifiées obtenues
la vie est une fête

-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 30 Sep 2019, 17:34
par akiwhite » 30 Sep 2019, 17:34
fatal_error a écrit:bj,
pour la une,
via table logique
En remarquant que la diff symétrique est le xor (je le représente par X)
- Code: Tout sélectionner
A|B|C|AXB|BXC|(AXB)XC|AX(BXC)
0|0|0| 0| 0| 0| 0
0|0|1| 0| 1| 1| 1
0|1|0| 1| 1| 1| 1
0|1|1| 1| 0| 0| 0
1|0|0| 1| 0| 1| 1
1|0|1| 1| 1| 0| 0
1|1|0| 0| 1| 0| 0
1|1|1| 0| 0| 1| 1
et on a bien les même lignes pour (AXB)XC et AX(BXC)
pour la 2), j'ai l'impression que l'égalité A∩(BΔC) = (A∩B)Δ(B∩C) est fausse:
- Code: Tout sélectionner
A|B|C|BXC|A(BXC)|AB|BC|(AB)X(BC)
0|0|0| 0| 0| 0| 0| 0
0|0|1| 1| 0| 0| 0| 0
0|1|0| 1| 0| 0| 0| 0
0|1|1| 0| 0| 0| 1| 0
1|0|0| 0| 0| 0| 0| 0
1|0|1| 1| 1| 0| 0| 0
1|1|0| 1| 1| 1| 0| 0
1|1|1| 0| 0| 1| 1| 1
A(BXC) et (AB)X(BC) n'ont pas les mêmes lignes
Merci pour ta réponse, je ne savais pas que l'on pouvait utiliser les tables de vérité (logique?) avec les ensembles.
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 30 Sep 2019, 17:35
par akiwhite » 30 Sep 2019, 17:35
fatal_error a écrit:wiki donne la def:
https://en.wikipedia.org/wiki/Exclusive_ormais je pense que ce qui est attendu est que tu te paluches la manipulation des U et ∩ en développant.
au pire du pire, je pense que tu peux simplifier les deux membres de l'égalité en somme de facteurs (genre F_1 UF_2 U F_3...) avec F_i que des "produits" d'intersections, etc, puis tu compares les deux formes simplifiées obtenues
Je crois bien que je ne sais pas du tout utiliser cette technique

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 30 Sep 2019, 17:58
par fatal_error » 30 Sep 2019, 17:58
Je crois bien que je ne sais pas du tout utiliser cette technique
que tu la connaisses ou pas, t'auras pas essayé bcp, en une minute

si je note AB pour dire A∩B, A+B pour AUB et
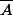
pour le complémentaire de A
on remarque déjà que

membre de gauche (AΔB)ΔC:
\Delta C = ((A\Delta B)\Delta \overline{C}) + (\overline{A\Delta B}C) = (A\overline{B}\overline{C}+\overline{A}B\overline{C}) +(ABC + \overline{AB}C )<br />= A\overline{B}\cap\overline{C}+\overline{A}\cap\overline{C}B + ABC + \overline{A}\cap\overline{B}C)
tu fais même chose pour le membre de droite AΔ(BΔC) et tu trouves normalement la même chose
edit: j'ai juste rajouté des symboles intersections pour qu'on confonde pas

la vie est une fête

-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 30 Sep 2019, 18:09
par akiwhite » 30 Sep 2019, 18:09
fatal_error a écrit: Je crois bien que je ne sais pas du tout utiliser cette technique
que tu la connaisses ou pas, t'auras pas essayé bcp, en une minute

si je note AB pour dire A∩B, A+B pour AUB et
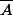
pour le complémentaire de A
on remarque déjà que

membre de gauche (AΔB)ΔC:
\Delta C = ((A\Delta B)\Delta \overline{C}) + (\overline{A\Delta B}C) = (A\overline{B}\overline{C}+\overline{A}B\overline{C}) +(ABC + \overline{AB}C )<br />= A\overline{B}\cap\overline{C}+\overline{A}\cap\overline{C}B + ABC + \overline{A}\cap\overline{B}C)
tu fais même chose pour le membre de droite AΔ(BΔC) et tu trouves normalement la même chose
edit: j'ai juste rajouté des symboles intersections pour qu'on confonde pas

A vrai dire je n'ai pas compris ce que tu voulais me faire essayer

-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 30 Sep 2019, 18:24
par akiwhite » 30 Sep 2019, 18:24
fatal_error a écrit: Je crois bien que je ne sais pas du tout utiliser cette technique
que tu la connaisses ou pas, t'auras pas essayé bcp, en une minute

si je note AB pour dire A∩B, A+B pour AUB et
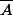
pour le complémentaire de A
on remarque déjà que

membre de gauche (AΔB)ΔC:
\Delta C = ((A\Delta B)\Delta \overline{C}) + (\overline{A\Delta B}C) = (A\overline{B}\overline{C}+\overline{A}B\overline{C}) +(ABC + \overline{AB}C )<br />= A\overline{B}\cap\overline{C}+\overline{A}\cap\overline{C}B + ABC + \overline{A}\cap\overline{B}C)
tu fais même chose pour le membre de droite AΔ(BΔC) et tu trouves normalement la même chose
edit: j'ai juste rajouté des symboles intersections pour qu'on confonde pas

Finalement je n'ai pas compris

\Delta C = ((A\Delta B)\Delta \overline{C}) + (\overline{A\Delta B}C))

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 30 Sep 2019, 18:40
par fatal_error » 30 Sep 2019, 18:40
j'ai juste appliqué la diff symétrique sur
)
et

la vie est une fête

-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 30 Sep 2019, 18:50
par akiwhite » 30 Sep 2019, 18:50
fatal_error a écrit:j'ai juste appliqué la diff symétrique sur
)
et

Ah oui pardon l'ecriture avec les + me perturbe my bad
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 30 Sep 2019, 19:04
par akiwhite » 30 Sep 2019, 19:04
fatal_error a écrit:j'ai juste appliqué la diff symétrique sur
)
et

Il y a une petite erreur je crois le tout premier delta est en fait un inter
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités



