1ereS : Probleme barycentres [résolu]
15 messages
- Page 1 sur 1
1ereS : Probleme barycentres [résolu]
Voila l'enoncé complet de l'exercice que je n'arrive pas a faire. Si quelqu'un sait comment faire dites le. Merci d'avance.
On considere un triangle ABC et O le centre de son cercle circonscrit.
Le point H est l'unique point du plan qui vérifie:
vecteur OH = vect OA + vect OB + vect OC
1) Montrer que H est l'orthocentre du triangle ABC.
2) G désigne le centre de gravité de ABC.
Les point O, G et H sont -ils alignés ?
On considere un triangle ABC et O le centre de son cercle circonscrit.
Le point H est l'unique point du plan qui vérifie:
vecteur OH = vect OA + vect OB + vect OC
1) Montrer que H est l'orthocentre du triangle ABC.
2) G désigne le centre de gravité de ABC.
Les point O, G et H sont -ils alignés ?
Salut,
considere G centre de gravité du triangle ABC donc
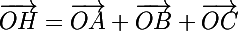
tu introduis le point G et tu devrais trouver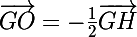
donc G est le centre d'une homothétie h de rapport (-1/2) transformant G en H.
on appelle I le milieu de [AB], on a la propriété : G est au 2/3 de [AI] ça signifie que h transforme I en C
Comme h conserve les angles, elle transforme la médiatrice (AI) en la hauteur issue de C.
tu fait pareil en appelant J milieu de [AC] et tu te rendras compte que H est sur les 2 hauteurs
2) c'est un resultat qui decoule de la 1ere question
sauf erreur
je te laisse finir
A+
considere G centre de gravité du triangle ABC donc
tu introduis le point G et tu devrais trouver
donc G est le centre d'une homothétie h de rapport (-1/2) transformant G en H.
on appelle I le milieu de [AB], on a la propriété : G est au 2/3 de [AI] ça signifie que h transforme I en C
Comme h conserve les angles, elle transforme la médiatrice (AI) en la hauteur issue de C.
tu fait pareil en appelant J milieu de [AC] et tu te rendras compte que H est sur les 2 hauteurs
2) c'est un resultat qui decoule de la 1ere question
sauf erreur
je te laisse finir
A+
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
