Comparaison d'intégrales convergentes

[MoonX]

Bonjour,

Soient trois fonction continue sur telles que :

- et convergent.
-

Peut-on affirmer que converge ?

J'ai cherché sans trouver. J'ai essayer de séparer en partie positive et négative comme pour la démo intégrable implique d'intégrale convergente mais sans succès (on ne peut rien conclure car l'intégrale des parties positives et négatives n'ont aucune raison de converger si la fonction n'est pas intégrable).

Je dois passer à côté d'un truc... Pouvez vous me guider ?

Je vous remercie par avance !

[aviateur]

Bonjour
La réponse est oui.
Preuve. On peut supposer sans restreindre la généralité que f=-h ( il suffit de tout translater de -(f+h)/2.).

Alors les hypothèses sont , i.e

Cela implique que g est absolument intégrable donc g intégrable.

[lionel52]

aviateur, h n'est pas forcément positive !

Sauf erreur
Tu peux essayer le critère de Cauchy : Soit comme les intégrales de f et h convergent alors, pour x assez grand et a > 0

[aviateur]

aviateur, h n'est pas forcément positive !

Je n'ai jamais dit cela!!

Je crois que tu n'as pas compris ma démo:
Par contre en translatant les fonctions de départ de -(f+h)/2, je m'y suis ramené.
C'est pas la même chose.
Le problème étant inchangé si on retire une fonction intégrable aux 3 fonctions. C'est ce que j'ai fait
car (f+h)/2 est intégrable.

[tournesol]

Je note le pour inférieur ou égal car je ne sais pas insérer du Latex .
On a f le g le h , donc -h le -g le -f .
On a donc 0 le g+ le h+ car g le h , et comme h+ est R intégrable , alors g+ est R intégrable .
On a aussi 0 le g- le f- car -g le -f , et comme f- est R intégrable , alors g- est R intégrable .
g est donc R intégrable .

[aviateur]

Bonjour
@tournesol: ta démonstration pose problème: à moins que tu y mettes des hypothèses supplémentaires.

l'hypothèse h est continue et l'intégrale est convergente signifie que l'intégrale de Riemann
admet une limite finie quand a tend vers et b tend vers

Ceci n'implique pas du tout que l'intégrale de est convergente et on peut trouver des contrexemples très simples.

Je pense qu'il faut rester sur ma démo. L'idée avec les restes de Cauchy fonctionne, c'est certain, mais pourquoi faire compliqué alors qu'on peut faire simple.

[tournesol]

Mea culpa aviateur , j'ai lu la question en diagonale et je n'ai retenu que la notation "intégrale sur R" qui est traditionnelement reservee aux fonctions intégrables (come somme sur N pour les familles sommables ) , ainsi que les expressions "partie positive" et "partie negative".
Je ne connaissais pas ta methode mais elle est plus elémentaire et abordable que le critère de Cauchy.
Pourrait tu profiter de cette question pour avoir l'amabilité de m'expliquer comment insérer du code Latex dans mon texte . Par avance merci .

[aviateur]

c'est très simple
méthode 1 "à la main "
par exemple \frac{1}{2} tu le mets à l'intérieur de 2 balises "tex"

[ "tex" ] ["/tex"] (ne pas mettre les "")


méthode 2

tu cliques dans éditeur complet, c'est plus pratique, et avec la souris , tu sélectionnes ton latex et tu cliques dans l'icône tex

[tournesol]

Merci a toi aviateur . Je vais essayer .

[tournesol]

[MoonX]

Merci pour vos réponses.
Cependant, je n'ai pas dans mon bagage le critère de Cauchy (bon, c'est bien sûr à ma portée, mais passant des concours, il faut que je sache faire sans).
Sinon pour la preuve d'Aviateur, je crois avoir compris (sommes nous d'accord, la translation c'est pas plutôt quelque chose du genre (f-h)/2 ? Parce que sinon, ça n'a aucune raison d'être de signe constant, et donc d'être intégrable ?)

Bref, en m'inspirant très très fortement de la preuve d'Aviateur, j'ai cette preuve là (est-elle juste ?)


est intégrable (car positive d'intégrale convergente).
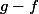
donc pas comparaison, est intégrable (ça ça ne pose pas pb, et c'est facile à redémontrer par croissance de l'intégrale dans le cas positif).

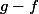
Donc a fortiori, est d'intégrale convergente (pour la preuve, c'est ce dont j'avais parlé dans mon post initial).

Et enfin, est alors d'intégrale convergente.

Ça me semble juste.

D'ailleurs, en parlant de Latex sur ce forum. Pourquoi n'est-il pas "mis à jour" ? Je veux dire par là, le système "Web" + Latex qu'on retrouve par exemple sur StackExchange n'a que des avantages... Écrire entre $ c'est beaucoup moins contraignant.

[aviateur]

Bonjour
Oui je crois que ta démo c'est ça.
quant à la mienne je retire (f+h)/2 aux 3 fonctions (dont l'intégrale sur R est convergente)

C'est à dire en explicitant


je pose

C'est à dire qu'on a alors avec intégrable. Alors j'ai démontré que dans ce cas g_1 est intégrable. Mais alors ça implique que g est intégrable (puisque j'ajoute (f+h)/2 à g_1 pour retrouver g)

Mais en gros ce que tu as fait revient un peu au même puis que tu retire f aux trois fonctions alors que moi je retire la moyenne de f et h