Bonjour j'ai un petit problème avec l'exercice suivant :
Soit (Un) une suite positive et décroissante. Prouver que si la série de terme générale Un converge alors nUn tend vers 0.
J'ai commencé avec un raisonnement par contraposée vous pensez que c'est un bon début?
Cordialement
Science
Séries convergentes
13 messages
- Page 1 sur 1
Salut,
Ben, pour le moment j'en pense pas grand chose, je ne vois pas de preuve, juste un tout petit début d'idée de preuve.
Bref, le sujet à été traité récemment [url="http://www.maths-forum.com/mp-un-resultat-suites-111562.php"]ici[/url].
Une autre manière de faire non proposée dans le topic précédent :
Soit epsilon fixé. A partir d'un certain rang,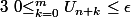 pour tout m et donc par décroissance,
pour tout m et donc par décroissance, U_{n+m}\le \epsilon) . On peut conclure directement en passant à la limite sup étant donné que
. On peut conclure directement en passant à la limite sup étant donné que 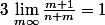 , on a que
, on a que U_{n+m}=\limsup_{m}\; \frac{m+1}{n+m}\times (n+m) U_{n+m}) si bien que
si bien que 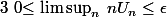 et donc
et donc 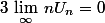
Ben, pour le moment j'en pense pas grand chose, je ne vois pas de preuve, juste un tout petit début d'idée de preuve.
Bref, le sujet à été traité récemment [url="http://www.maths-forum.com/mp-un-resultat-suites-111562.php"]ici[/url].
Une autre manière de faire non proposée dans le topic précédent :
Soit epsilon fixé. A partir d'un certain rang,
Science a écrit:Bonjour j'ai un petit problème avec l'exercice suivant :
Soit (Un) une suite positive et décroissante. Prouver que si la série de terme générale Un converge alors nUn tend vers 0.
J'ai commencé avec un raisonnement par contraposée vous pensez que c'est un bon début?
Cordialement
Science
Oui, c'est un début tout à fait pertinent.
Sinon, si tu veut une preuve "directe", il y a plusieurs idées là :
http://www.maths-forum.com/showthread.php?t=111562
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Au passage, j'en profite pour donner cette généralisation (que j'ai déjà proposée sur le forum je crois) toujours intéressante à étudier :
Si_{n}) est une suite de 1 et de -1 telle que
est une suite de 1 et de -1 telle que 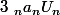 est convergente, toujours sous les hypothèses que
est convergente, toujours sous les hypothèses que ) est une suite réelle décroissante, alors
est une suite réelle décroissante, alors U_{n}=0)
(ton exercice étant le cas particulier où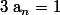 pour tout n.)
pour tout n.)
Si
(ton exercice étant le cas particulier où
Au fait je n'ai pas vu les séries de Cauchy en cours (mais je sais quand même ce que sait) donc je peux pas faire la preuve "directe"
Voilà ce que je fais si nUn ne tend pas vers 0 alors nécessairement la série de terme générale nUn diverge, à partir de là je dois en déduire que la série de terme général Un diverge (avec Un respectant les hypothèses) mais c'est là où je bloque
Voilà ce que je fais si nUn ne tend pas vers 0 alors nécessairement la série de terme générale nUn diverge, à partir de là je dois en déduire que la série de terme général Un diverge (avec Un respectant les hypothèses) mais c'est là où je bloque
Science a écrit:Au fait je n'ai pas vu les séries de Cauchy en cours (mais je sais quand même ce que sait) donc je peux pas faire la preuve "directe"
Voilà ce que je fais si nUn ne tend pas vers 0 alors nécessairement la série de terme générale nUn diverge, à partir de là je dois en déduire que la série de terme général Un diverge (avec Un respectant les hypothèses) mais c'est là où je bloque
C'est normal tu affaiblis trop l'hypothèse (dire que
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
