Bonjour,
Je suis en 1°année d'économie et droit et je voudrais un renseignement sur un exercice de la microéconomie:
Je sais que je suis dans un forum mathématique mais l'exercice demande une réfléxion mathématique.
Il s'intitule : résoudre max (x,y) x+y sous contrainte x^2 + y^2 =< 10
Je sais qu'il faut trouver la dérivée puis la dérivée seconde, il y a une histoire de concavité mais ...
(quel est le max ou autre ??)
Merci beaucoup pour votre aide
club@olivierb.net
Contrainte budgétaire
7 messages
- Page 1 sur 1
En fait c'est simple.
Tu pose f(x,y)=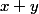 et h(x,y)=
et h(x,y)=
puis tu calcules le gradient de f (c'est-à-dire la dérivée de f en x et en y), puis enfin tu calcule le hessien de f.
Si ce dernier est définie négatif alors f est strictement concave, ainsi il te suffit de résoudre grad(f)+z.grad(h) =0 pour la solution optimale...
Mais ici il n'y a pas besoin de ce donner tant de mal, on voit que x et y sont symétrique, c'est-à-dire que l'équation reste vérifié si tu remplace x par y et vis versa. Donc ton problème se remène a :

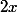

ou

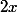

donc

Tu pose f(x,y)=
puis tu calcules le gradient de f (c'est-à-dire la dérivée de f en x et en y), puis enfin tu calcule le hessien de f.
Si ce dernier est définie négatif alors f est strictement concave, ainsi il te suffit de résoudre grad(f)+z.grad(h) =0 pour la solution optimale...
Mais ici il n'y a pas besoin de ce donner tant de mal, on voit que x et y sont symétrique, c'est-à-dire que l'équation reste vérifié si tu remplace x par y et vis versa. Donc ton problème se remène a :
ou
donc
réponse ajout
Merci beaucoup pour votre aide si précieuse
Je vous envoie mon ébauche de travail tout de meme
En effet la contrainte budgétaire signifie le revenu en gros.
pour ma part
max (x,y) x+y sous la contrainte budgétaire : x² + y²=< 1
y² =< 1-x² puis 1. y =< racine (1-x²) ou bien 2. y=< - (racine (1-x²)
ensuite j'ai remplacé dans la fonction x + racine(1-x²) ou x- racine( 1-x²)
j'ai calculé la dérivée : f'(x) = (2 racine (1-x²) - 2x ) / (2 racine(1-x²)
ensuite il faut calculer la dérivée seconde f''(x) = Trop de mal ... (si quelqu'un à la dérivée seconde de cette bete la lol)...
et dire si elle est concave ou convexe et de montrer qu'il y a un ou plusieurs maximums ou minimums . voila
J'espère que cela est bon, ( a vérifier )
Encore merci pour vos aides
club@olivierb.net
Je vous envoie mon ébauche de travail tout de meme
En effet la contrainte budgétaire signifie le revenu en gros.
pour ma part
max (x,y) x+y sous la contrainte budgétaire : x² + y²=< 1
y² =< 1-x² puis 1. y =< racine (1-x²) ou bien 2. y=< - (racine (1-x²)
ensuite j'ai remplacé dans la fonction x + racine(1-x²) ou x- racine( 1-x²)
j'ai calculé la dérivée : f'(x) = (2 racine (1-x²) - 2x ) / (2 racine(1-x²)
ensuite il faut calculer la dérivée seconde f''(x) = Trop de mal ... (si quelqu'un à la dérivée seconde de cette bete la lol)...
et dire si elle est concave ou convexe et de montrer qu'il y a un ou plusieurs maximums ou minimums . voila
J'espère que cela est bon, ( a vérifier )
Encore merci pour vos aides
club@olivierb.net
demande
Bonjour,
Je voulais encore un petit renseignement
(x,y) x+y sous la contrainte budgétaire : x² + y² =< 1
Ais-je le droit de poser x + y =< racine 1 ??? en vue de la contrainte
Car aprés c'est terriblement long et ce n'est pas du tout le meme topo, je voulais savoir si c'était possible
Merci beaucoup
Olivier
club@olivierb.net
Je voulais encore un petit renseignement
(x,y) x+y sous la contrainte budgétaire : x² + y² =< 1
Ais-je le droit de poser x + y =< racine 1 ??? en vue de la contrainte
Car aprés c'est terriblement long et ce n'est pas du tout le meme topo, je voulais savoir si c'était possible
Merci beaucoup
Olivier
club@olivierb.net
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
