SYSTEME D'EQUATION

[harsisi]

Salut à tous, besoin d'aide pour la résolution du systeme suivant
x|x|+y|y|=1
E(x)+E(y)=1

[chan79]

salut
Tu as fais quoi pour l'instant ?
A priori, je chercherais d'abord les solutions (x,y) telles que x>=0 et y>=0

[harsisi]

je ne connais pas comment utiliser la 2e equation du systeme

[Carpate]

[mathelot]

Non pour x négatif, on a la même définition de E que pour les x positifs.
pour x<0 ce qui donne pour -3.5 une partie entière de -4

[harsisi]

Et ensuite stp?

[mathelot]

Et ensuite stp?

je reprécise que c'est faux

[chan79]

si x>=0 et y>=0, la première égalité devient x²+y²=1
On montre facilement qu'il y a deux solutions: (1,0) et (0,1)

Pour la suite, on remarque que si (x,y) est solution alors (y,x) aussi
deux autres cas à envisager

[Black Jack]

Et ensuite stp?

Salut,

mathelo t'a fait remarquer que c'était faux ... et donc ne pas partir de là.

Aide :

On peut partir ainsi :

Montrer que on a obligatoirement au moins une des 2 variables > 0

Comme x et t sont interchangeables dans le système d'équations, on peut limiter l'étude à x >= 0

a) si x = 0, on a y = 1

b) si 0 < x < 1, |x|=x et E(x) = 0
--> E(y) = 1 et donc 0 < y < 2, |y| = y

x² + y² = 1 --> 0 < y² < 1 --> E(y) = 0 (impossible)

c) Si x = 1
y|y| = 0
E(y) = 0
Et donc x=1 et y= 0 convient.

d) Si x > 1, |x|=x
x|x|=x² > 1 et donc y|y|<0 --> y < 0 et |y|=-y

Essaie de continuer ... on est presque au bout.

[pascal16]

je pense que le "c'est faux" se reportait aux inéquations. L'une est strict et l'autre large.

[Carpate]

J'étais tombé dans le piège d'une la pseudo-évidence !
En revenant(relisant) à la définition de la partie entière d'un réel : le plus petit entier n tel que , pour tout réel x (positif ou négatif) :
E(-3,8) = -4
Edit
je n'avais pas vu les corrections précédentes de mathelot ...

[Ben314]

Salut

x|x|+y|y|=1
E(x)+E(y)=1

C'est de nouveau pas bien méchant :
Si on considère que et qu'on pose alors donc .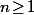
Si on écrit ensuite avec , alors on a :

Donc on a forcémen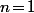t et 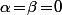, c'est à dire 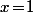et .

P.S. : Et, à mon sens, "la" définition de E(x), c'est que c'est "le plus grand entier inférieur ou égal à " qui existe du fait que toute partie non vide de N admet un plus élément élément ce qui implique que toute partie majorée de Z admet un plus grand élément.

[chan79]

harsisi peut dire merci.
Il a réussi à avoir des solutions détaillées sans montrer le moindre début de tentative de recherche ....

[Ben314]

Oui, mais je suis à peu prés sûr que c'est pas des truc scolaires : ça sent nettement plus le truc style "kangourou mathématique" ou quelque chose du même style pour collégiens (mais bon, c'est plutôt fait pour les bons collégiens et là harsisi, ça a pas l'air d'être trop son cas . . . )