Ok Aviateur je mets l'énoncé complet. J'ai demandé sur un autre forum de l'aide mais personne n'a réussi à trouver la réponse. Ça fait une journée que je suis dessus ma tête va exploser.
Je suis dans une démonstration pour montrer le théorème suivant mais je pense qu'il y a une petite erreur :
Théorème : Soit  un intervalle. La bijection réciproque
un intervalle. La bijection réciproque  d'une fonction continue et strictement monotone sur I est continue sur
d'une fonction continue et strictement monotone sur I est continue sur )
.
On a démontré juste avant (pas de souci pour cette démo) que :
la bijection réciproque de tout fonction continue sur  et strictement monotone sur
et strictement monotone sur  est strictement monotone sur
est strictement monotone sur ) et de même sens de variation que
et de même sens de variation que  .
.Supposons que

est strictement croissante sur

. Fixons
)
Soit
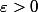
Nous devons montrer que

est continue soit :
, |y-y_0| < \eta \Rightarrow |f^{-1}(y)-f^{-1}(x_0)| < \varepsilon)
Notons :
) Premier cas :
Premier cas : )
Dans ce cas,
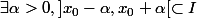
Notons :
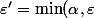)
Ainsi :
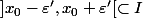
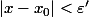

 <f( x) < f(x_0 + \varepsilon'))
Pas compris comment on peut passer à la croissante de f car on sait pas si
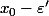
et
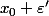
sont des éléments de

!
Il faudrait peut être prendre :
}{2})
? C'est une proposition de ma part...
Notons
)
et
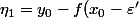 >0)
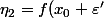 - y_0 >0)
Comment on a-t-on le droit d'écrire :
)
? On ne sait pas si
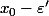
appartient à l'ensemble de définition de

...
Ainsi :
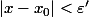

On a obtenu :
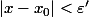

On sait que :
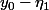
et
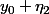
sont dans
)
Comme f est continue sur

alors
)
est un intervalle et donc :
)
Si on pose :
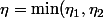)
on obtient :
)
Ainsi on a :
)
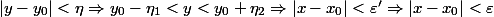
C'est-à-dire :
-f^{-1}(y_0)| < \varepsilon) 2ème cas :
2ème cas : 
est une borne de

. (le cas où

est la borne supérieure de

s'adapte facilement). Notons que comme

est strictement croissante sur

,

est la borne inférieure de
)
.
Dans ce cas :

Je pense que c'est la caractérisation de la borne inférieure et au lieu du pour tout alpha strictement positif on met "il existe" car on veut rester dans

.
Notons
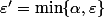
ainsi :
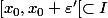
Idem je prendrais
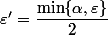
La suite de la démo est analogue au 1er cas donc si je comprends le premier cas je comprendrai celui-ci.
un intervalle et
une fonction strictement croissante.
est un intervalle mais vu que je sais pas si c'est un segment je vois pas comment montrer que
est la borne inférieure de
.