Bonjour,
Je reprends mes études à la rentrée 2018 en Fac de science après quelques années passé dans la vie active. Je revois donc les programmes des matières qui me seront nécessaires pour la rentrée. Je suis actuellement sur le programme de mathématiques de terminale S. Je bloque sur deux exercices sur les limites de suites :
Exercice 1
Soit la suite u définie par u0 = 5 et un+1 = √(3un + 1) (la racine englobe 3un + 1)
1. Montrer que (un) est décroissante.
2. Montrer que la suite (un) est minorée.
3. En déduire que la suite (un) est convergente.
Exercice 2
Soit la suite (un) définie par u0 = 0 et un+1 = √(un + 5) (la racine englobe un + 5)
1. Montrer que cette suite est croissante.
2. Montrer que pour tout entier n, 0 ≤ un ≤ 3. En d´éduire que la suite (un) est convergente.
3. Déterminer la limite l de la suite (un).
J'aimerais qu'on ne donne pas la solution, juste qu'on me guide dans un premier temps, pour essayer de comprendre la démarche et le raisonnement à suivre.
Je vous remercie par avance de votre aide.
[Terminale S] Limite d'une suite
10 messages
- Page 1 sur 1
Re: [Terminale S] Limite d'une suite
Soit la suite u définie par u0 = 5 et un+1 = √(3un + 1) (la racine englobe 3un + 1)
1. Montrer que (un) est décroissante.
perso, je dirais " on peut remarquer que Un>1 pour tout n, donc je peux élever au carré pour comparer"
1. Montrer que (un) est décroissante.
perso, je dirais " on peut remarquer que Un>1 pour tout n, donc je peux élever au carré pour comparer"
Re: [Terminale S] Limite d'une suite
Bonjour,
1. Tu peux aussi calculer et remarquer que la fonction
et remarquer que la fonction  telle que
telle que ) est croissante. Ceci veut dire que si
est croissante. Ceci veut dire que si  , alors
, alors  \leq f(u_0)=u_1) , etc...
, etc...
Donc une récurrence peut faire l'affaire.
1. Tu peux aussi calculer
Donc une récurrence peut faire l'affaire.
Re: [Terminale S] Limite d'une suite
Merci de vos réponses !
Je pense avoir réussi à répondre la question 1 de l'exercice 1 (et donc pouvoir faire également la question 1 de l'exercice 2).
Je vous montre ma réponse :
Je vais montrer que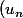) est décroissante par récurrence.
est décroissante par récurrence.
Initialisation : Je calcule
donc
Hérédité : Je suppose que
) où
où =\sqrt{3x+1}) ,
, ) est croissante
est croissante
alors
donc
Conclusion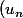) est décroissante
est décroissante
Je pense avoir réussi à répondre la question 1 de l'exercice 1 (et donc pouvoir faire également la question 1 de l'exercice 2).
Je vous montre ma réponse :
Je vais montrer que
Initialisation : Je calcule
donc
Hérédité : Je suppose que
alors
donc
Conclusion
Re: [Terminale S] Limite d'une suite
la rédaction me laisse supposer que tu n'as peut être pas compris la subtilité :
f croissante => f conserve l'ordre
on suppose Un>Un+1
donc
3U(n) > 3 U(n+1)
donc
3U(n) +1 > 3 U(n+1)+ 1
comme la fonction racine est croissante sur R+ (et que les termes sont positifs)
√(3U(n) +1) > √(3 U(n+1)+ 1 )
soit
Un+1 > Un+2
on se sert de la relation directe avec
Un+1 =f(Un)
et g(x) = f(x)-x, g positive
f croissante => f conserve l'ordre
on suppose Un>Un+1
donc
3U(n) > 3 U(n+1)
donc
3U(n) +1 > 3 U(n+1)+ 1
comme la fonction racine est croissante sur R+ (et que les termes sont positifs)
√(3U(n) +1) > √(3 U(n+1)+ 1 )
soit
Un+1 > Un+2
on se sert de la relation directe avec
Un+1 =f(Un)
et g(x) = f(x)-x, g positive
Re: [Terminale S] Limite d'une suite
Bonjour
Je trouve deux erreurs dans le raisonnement.
La première erreur est un non-dit sauf (excepté que dans une réponse ce n'est pas dit mais sous-entendu). C'est disons une petite omission . En effet si je considère un exercice presque identique mais avec et
et  cela devrait faire comprendre tout de même qu'il y a une précision à faire.
cela devrait faire comprendre tout de même qu'il y a une précision à faire.
La deuxième erreur est pour moi plus importante: la phrase "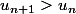 et f croissante implique
et f croissante implique >f(u_n)) est fausse. "
est fausse. "
Je trouve deux erreurs dans le raisonnement.
La première erreur est un non-dit sauf (excepté que dans une réponse ce n'est pas dit mais sous-entendu). C'est disons une petite omission . En effet si je considère un exercice presque identique mais avec
La deuxième erreur est pour moi plus importante: la phrase "
Re: [Terminale S] Limite d'une suite
Bonjour,
Il faut montrer effectivement que la suite est bien définie : facile avec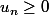 pour tout
pour tout  .
.
Il faut surtout montrer que est croissante (pas fait), ou bien utiliser la méthode de @pascal qui évite de le faire.
est croissante (pas fait), ou bien utiliser la méthode de @pascal qui évite de le faire.
Il faut montrer effectivement que la suite est bien définie : facile avec
Il faut surtout montrer que
Re: [Terminale S] Limite d'une suite
Surtout ce que je veux dire que f "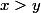 et f croissante implique
et f croissante implique \geq f(y)) "
"
( et non pas > )
( et non pas > )
Re: [Terminale S] Limite d'une suite
je rectifie :
la rédaction me laisse supposer que tu n'as peut être pas compris la subtilité :
f croissante => f conserve l'ordre
f strictement croissante => f conserve l'ordre au sens stricte
on suppose Un>Un+1
donc
3U(n) > 3 U(n+1)
donc
3U(n) +1 > 3 U(n+1)+ 1
comme la fonction racine est strictement croissante sur R+ (et que les termes sont positifs), elle conserve l'ordre au sens stricte.
√(3U(n) +1) > √(3 U(n+1)+ 1 )
soit
Un+1 > Un+2
on se sert de la relation directe avec
Un+1 =f(Un)
et g(x) = f(x)-x, g positive (ou strictement positive)
la rédaction me laisse supposer que tu n'as peut être pas compris la subtilité :
f croissante => f conserve l'ordre
f strictement croissante => f conserve l'ordre au sens stricte
on suppose Un>Un+1
donc
3U(n) > 3 U(n+1)
donc
3U(n) +1 > 3 U(n+1)+ 1
comme la fonction racine est strictement croissante sur R+ (et que les termes sont positifs), elle conserve l'ordre au sens stricte.
√(3U(n) +1) > √(3 U(n+1)+ 1 )
soit
Un+1 > Un+2
on se sert de la relation directe avec
Un+1 =f(Un)
et g(x) = f(x)-x, g positive (ou strictement positive)
Re: [Terminale S] Limite d'une suite
NB : pour la suite
(Un croissante ou Un strictement croissante) et majorée => Un converge
est vrai
(Un croissante ou Un strictement croissante) et majorée => Un converge
est vrai
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 120 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
