Bonsoir !
Je me fais quelques exercices en spé maths sur le chapitre de divisibilité (car j'ai quelques difficultés). Voici l'exercice qui me pose problème :
m et n sont deux entiers relatifs.
On pose a = 10n + m.
1) Démontrez que si n - 11m est divisible par 37, alors a est divisible par 37.
2) La réciproque de cette proposition est-elle vraie ?
A vrai dire, il n'y a que la deuxième question qui coince. On peut conjecturer qu'elle est juste mais je ne vois vraiment pas comment le démontrer.
Merci !
DIVISEURS COMMUNS (Terminale S Spé)
5 messages
- Page 1 sur 1
Re: DIVISEURS COMMUNS (Terminale S Spé)
Bonsoir,
Oui la réciproque est correcte car :
si \rightarrow 37k = 10n+m) avec
avec 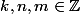
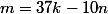
Si on remplace dans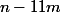 on obtient
on obtient
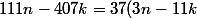)
donc
 \leftrightarrow 37|(10n+m))
Cordialement.
Oui la réciproque est correcte car :
si
Si on remplace dans
donc
Cordialement.
Modifié en dernier par FLBP le 29 Sep 2017, 20:30, modifié 1 fois.
Re: DIVISEURS COMMUNS (Terminale S Spé)
Merci beaucoup ! Je ne connaissais pas cette méthode. Il est toujours bon d'apprendre 
Re: DIVISEURS COMMUNS (Terminale S Spé)
Cet exercice est intéressant car il permet (en particulier) de dire si un nombre a est multiple de 37.
Prenons un exemple a=148. On le met sous la forme 10n+m(division euclidienne par 10 par exemple)
148=10*14+8 donc n=14 et m=8
Comme n-11m=14-88=74=37*2 est divisible par 37 alors a = 148 l'est aussi.
Et puis si le nombre est très gros, on peut réitérer le processus!
a = 4773 est il multiple de 37?
a= 477×10+3
n=477 et m=3
n-11m=477-33=444
Or 444=10*44+4
n-11m=44-44=0
Donc 444 est multiple de 37.
Donc 4773 est multiple de 37
Prenons un exemple a=148. On le met sous la forme 10n+m(division euclidienne par 10 par exemple)
148=10*14+8 donc n=14 et m=8
Comme n-11m=14-88=74=37*2 est divisible par 37 alors a = 148 l'est aussi.
Et puis si le nombre est très gros, on peut réitérer le processus!
a = 4773 est il multiple de 37?
a= 477×10+3
n=477 et m=3
n-11m=477-33=444
Or 444=10*44+4
n-11m=44-44=0
Donc 444 est multiple de 37.
Donc 4773 est multiple de 37
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: DIVISEURS COMMUNS (Terminale S Spé)
Salut,
Ca revient plus ou moins au même, mais perso., j'aurais écrit que, si a = 10n + m et b=n-11m alors a-10b=(10n+m)-10(n-11m)=111m=3x37m
(évidement je calcule a-10b de façon à éliminer les n. On peut à la place calculer 11a+b de façon à éliminer les m)
Ensuite,
- Si 37 divise b alors il divise 10b+3x37m qui vaut a
- Réciproquement, si 37 divise a alors il divise a-3x37m qui vaut 10b et, comme 37 est premier avec 10, c'est qu'il divise b.
On peut aussi remarquer que la même preuve montre que 3 divise a ssi 3 divise b et que 111 divise a ssi 111 divise b.
Ca revient plus ou moins au même, mais perso., j'aurais écrit que, si a = 10n + m et b=n-11m alors a-10b=(10n+m)-10(n-11m)=111m=3x37m
(évidement je calcule a-10b de façon à éliminer les n. On peut à la place calculer 11a+b de façon à éliminer les m)
Ensuite,
- Si 37 divise b alors il divise 10b+3x37m qui vaut a
- Réciproquement, si 37 divise a alors il divise a-3x37m qui vaut 10b et, comme 37 est premier avec 10, c'est qu'il divise b.
On peut aussi remarquer que la même preuve montre que 3 divise a ssi 3 divise b et que 111 divise a ssi 111 divise b.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 94 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
