Soit a un entier supérieur ou égal à 2.
Comment démontrer que
Déjà on sait que
Limite logarithme
12 messages
- Page 1 sur 1
Limite logarithme
par mehdi-128 » 01 Sep 2017, 15:45
Bonjour,
Soit a un entier supérieur ou égal à 2.
Comment démontrer que}{x^{a-\frac{3}{2}}})
Déjà on sait que
Soit a un entier supérieur ou égal à 2.
Comment démontrer que
Déjà on sait que
Re: Limite logarithme
par MJoe » 01 Sep 2017, 15:59
Bonjour @Mehdi-128 et bonjour à tous,
Il faut utiliser les résultats sur ce que l'on appelle "le théorème des croissances comparées".
Plus de détails.
Je commence :
On a, pour tout réel
: 
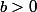
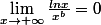
et pour 
: 
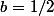
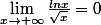
MJoe.
Il faut utiliser les résultats sur ce que l'on appelle "le théorème des croissances comparées".
Plus de détails.
Je commence :
On a, pour tout réel
MJoe.
Re: Limite logarithme
par zygomatique » 01 Sep 2017, 16:28
salut
...
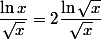
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Limite logarithme
par mehdi-128 » 02 Sep 2017, 11:55
Je comprends pas trop pourquoi vous utilisez la racine carrée ...
J'ai :}{x^b})
où 
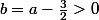
Donc par croissance comparée elle vaut 0 c'est direct non ?
J'ai :
Donc par croissance comparée elle vaut 0 c'est direct non ?
Re: Limite logarithme
par Pseuda » 02 Sep 2017, 12:20
Bonjour,
Oui avec le théorème de croissance comparée, on a très directement le résultat. Je pense que @zygomatique donne une solution si on ne le connait pas (lycée).
Oui avec le théorème de croissance comparée, on a très directement le résultat. Je pense que @zygomatique donne une solution si on ne le connait pas (lycée).
Re: Limite logarithme
par mehdi-128 » 02 Sep 2017, 12:29
Oui je vois mais quel est le rapport entre : 
et 
Re: Limite logarithme
par zygomatique » 02 Sep 2017, 12:41
la seule croissance comparée connue en terminale est ln x / x --> 0 quand x --> +oo
je me ramène donc toujours à cette forme qui permet évidemment d'obtenir le résultat pour tout puissance de x (du dénominateur) ...
je me ramène donc toujours à cette forme qui permet évidemment d'obtenir le résultat pour tout puissance de x (du dénominateur) ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Limite logarithme
par FLBP » 02 Sep 2017, 15:58
Salut,
Si tu veux en avoir le cœur net, tu peux remplacer (pour faciliter - légèrement- la compréhension)
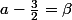
sachant que
Et utiliser la règle de Bernoulli-l'Hospital :
}{x^\beta} = \lim_{x\to \infty} \frac{(\ln(x))'}{(x^\beta)'} = \lim_{x\to \infty} \frac{\frac{1}{x}}{(\beta + 1)x^{\beta-1}} = \lim_{x\to \infty} \frac{1}{(\beta + 1)x^{\beta}} = 0)
Cordialement.
Si tu veux en avoir le cœur net, tu peux remplacer (pour faciliter - légèrement- la compréhension)
Et utiliser la règle de Bernoulli-l'Hospital :
Cordialement.
Modifié en dernier par FLBP le 02 Sep 2017, 17:26, modifié 1 fois.
Re: Limite logarithme
par zygomatique » 02 Sep 2017, 16:19
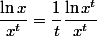
+ mon post précédent ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Limite logarithme
par mehdi-128 » 02 Sep 2017, 16:21
zygomatique a écrit:la seule croissance comparée connue en terminale est ln x / x --> 0 quand x --> +oo
je me ramène donc toujours à cette forme qui permet évidemment d'obtenir le résultat pour tout puissance de x (du dénominateur) ...
Ah enfin compris merci
Re: Limite logarithme
par MJoe » 03 Sep 2017, 08:13
Bonjour,
Malheureusement, je crois que la règle de Bernoulli-L'Hospital n'est pas enseignée au lycée, en série S.
MJoe.
Malheureusement, je crois que la règle de Bernoulli-L'Hospital n'est pas enseignée au lycée, en série S.
MJoe.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :