Lycée: Fonctions et étude de signe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
MJoe
- Membre Relatif
- Messages: 295
- Enregistré le: 19 Juil 2017, 06:26
- Localisation: Saint-Nazaire
-
 par MJoe » 30 Aoû 2017, 17:47
par MJoe » 30 Aoû 2017, 17:47
Bonjour,
Pour la )b, il faudra prendre les intervalles où
\leq0)
afin de répondre à la question. Mais pour cela il faut revoir ton tableau de signe.
Pour la 3)c) : Cela me semble bien mais tu as mis 3)b) sur ta feuille scannée.
MJoe.
Modifié en dernier par
MJoe le 30 Aoû 2017, 17:49, modifié 1 fois.

-
MJoe
- Membre Relatif
- Messages: 295
- Enregistré le: 19 Juil 2017, 06:26
- Localisation: Saint-Nazaire
-
 par MJoe » 30 Aoû 2017, 17:48
par MJoe » 30 Aoû 2017, 17:48
Bonjour,
Pour ajouter une ligne

c'est facile :

vaut zéro en zéro, il est négatif "à gauche" de 0 et positif "à droite".
MJoe.

-
MJoe
- Membre Relatif
- Messages: 295
- Enregistré le: 19 Juil 2017, 06:26
- Localisation: Saint-Nazaire
-
 par MJoe » 30 Aoû 2017, 17:57
par MJoe » 30 Aoû 2017, 17:57
Voici un exemple de tableau (j'ai modifié le tien) :
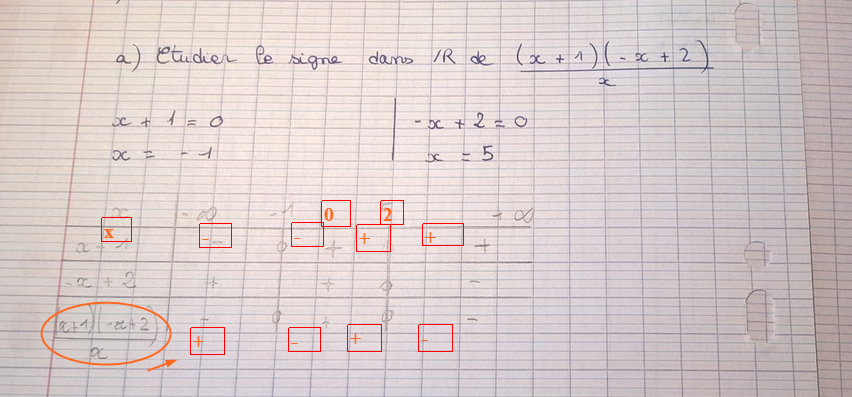
MJoe.
-
Antonin
- Membre Naturel
- Messages: 37
- Enregistré le: 25 Aoû 2017, 18:06
-
 par Antonin » 30 Aoû 2017, 18:19
par Antonin » 30 Aoû 2017, 18:19
Salut Mjoe,
Ok pour le tableau avec x et merci beaucoup! Ce matin l'image que j'ai mise à disposition contenait le 3) petit c où j'ai mis : ]2+ l'infini[ U ]-1;- l'infini ( je doute) [
Pour le 1) Pseuda m'as donné une piste mais je n'arrive pas à le résoudre ma technique ne marche pas...

-
MJoe
- Membre Relatif
- Messages: 295
- Enregistré le: 19 Juil 2017, 06:26
- Localisation: Saint-Nazaire
-
 par MJoe » 30 Aoû 2017, 18:43
par MJoe » 30 Aoû 2017, 18:43
Bonsoir,
Ton interprétation me semble juste (question 3)c) du sujet).
Pour ce qui est de l'intervalle (suite à ton tableau de signes), vérifie que tu obtiens :

Voir les parties encadrées
en vert ci-dessous :
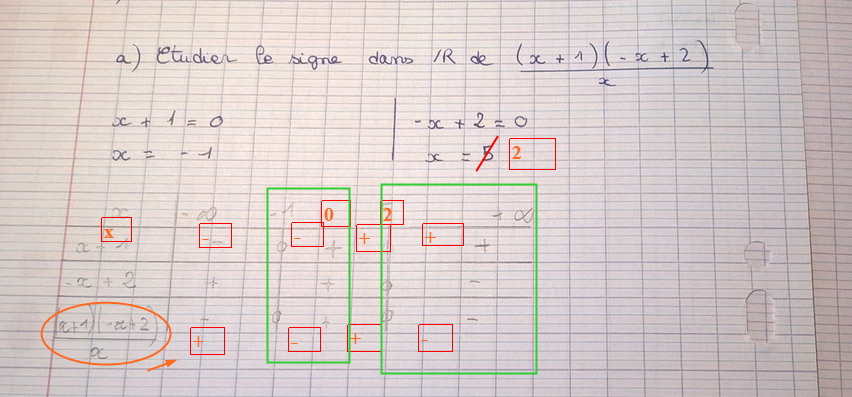
MJoe.
-
Antonin
- Membre Naturel
- Messages: 37
- Enregistré le: 25 Aoû 2017, 18:06
-
 par Antonin » 31 Aoû 2017, 10:31
par Antonin » 31 Aoû 2017, 10:31
salut Mjoe,
Merci beaucoup! tu n'aurais pas une piste à me donner pour le 1)?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 31 Aoû 2017, 11:03
par zygomatique » 31 Aoû 2017, 11:03
quand on fait une étude de signe ce n'est pas la nullité (d'un facteur) qui nous intéresse c'est son signe !!
avec
 = \dfrac {(x + 1)(2 - x)} x)
je résous donc :



(un nombre est positif quand il est positif et ce nombre n'est pas nul puisque ""c'est un dénominateur"")
je sais ainsi où je mets des + dans mon tableau de signe
d'autre part après une première on peut même aller un peut plus vite quand on a vu les trinomes du second degré et leur signe :
(2 - x) \ge 0 \iff -1 \le x \le 2)
ce qui fait une ligne de moins dans le tableau de signe ...
le tableau de mjoe est faux : il manque la valeur 0 (avec une double barre car ""valeur interdite"") et le signe de x ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
MJoe
- Membre Relatif
- Messages: 295
- Enregistré le: 19 Juil 2017, 06:26
- Localisation: Saint-Nazaire
-
 par MJoe » 31 Aoû 2017, 16:30
par MJoe » 31 Aoû 2017, 16:30
zygomatique a écrit:le tableau de mjoe est faux : il manque la valeur 0 (avec une double barre car ""valeur interdite"") et le signe de x ...
Bonjour à tous,
Je n'ai juste fait que d'ajouter les signes sur le tableau d'Antonin. Oui effectivement il manque les doubles barres en 0. L'idée c'était de "débloquer" Antonin sur le signe de "x" dans ce tableau sans refaire tout le tableau de signes.
MJoe

Modifié en dernier par
MJoe le 31 Aoû 2017, 16:43, modifié 1 fois.

-
MJoe
- Membre Relatif
- Messages: 295
- Enregistré le: 19 Juil 2017, 06:26
- Localisation: Saint-Nazaire
-
 par MJoe » 31 Aoû 2017, 16:39
par MJoe » 31 Aoû 2017, 16:39
Antonin a écrit:salut Mjoe,
Merci beaucoup! tu n'aurais pas une piste à me donner pour le 1)?
Bonjour Antonin,
Je pensais que tu avais déjà traité la question 1).
Alors il s'agit de déterminer l'expression de
=f(x)-g(x))
On a :
 = \frac{2}{x}-(x-1))
. Ensuite on réduit au même dénominateur :
 = \frac{2}{x}-\frac{x(x-1)}{x})
, d'où
=\frac{2-x(x-1)}{x}=\frac{-x^{2}+x+2}{x})
Il reste alors à factoriser le polynôme :

Pour la factorisation, il y a ce document qui peut t'aider :
Télécharger ce document.
Dis-moi si tu t'en sors.
MJoe.
-
Antonin
- Membre Naturel
- Messages: 37
- Enregistré le: 25 Aoû 2017, 18:06
-
 par Antonin » 01 Sep 2017, 17:07
par Antonin » 01 Sep 2017, 17:07
Salut MJoe,
Un grand merci pour l'aide que tu m'apportes! Cela me paraît étrange qu'un prof de seconde donne cet exercice si on est obligé de" factoriser le polynôme " notion même pas abordée. J'ai essayer de comprendre le document mais c'est très complexe il n'y a pas un moyen plus simple de répondre au 1)? ( j'ai peur que mon prof s'interroge sur le fait que j'utilise une notion que je n'ai pas abordé en seconde...)
Bonne soirée


-
MJoe
- Membre Relatif
- Messages: 295
- Enregistré le: 19 Juil 2017, 06:26
- Localisation: Saint-Nazaire
-
 par MJoe » 01 Sep 2017, 17:22
par MJoe » 01 Sep 2017, 17:22
Bonjour Antonin,
Oh ! Je ne savais pas que tu n'avais pas vu la factorisation. Effectivement c'est bizarre que l'on te demande (indirectement) de faire une factorisation.
Et c'est vrai, tu ne peux pas utiliser le document joint ci-avant pour factoriser puisque tu ne l'as pas vu en cours.
Alors comment faire ?
Voici ce que tu pourrais dire :
On remarque que
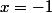
est solution de l'équation

On peut donc écrire ce polynôme sous la forme
(-x+c))
Puis ensuite développer et déterminer

par identification.
MJoe.

-
MJoe
- Membre Relatif
- Messages: 295
- Enregistré le: 19 Juil 2017, 06:26
- Localisation: Saint-Nazaire
-
 par MJoe » 01 Sep 2017, 17:42
par MJoe » 01 Sep 2017, 17:42
Encore moi Antonin,
J'ai une autre idée : est-ce que tu as vu la forme canonique ?
Il s'agit d'écrire

comme le début d'un carré :
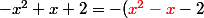=-({\color{red}(x-1/2)^{2}-1/4} -2)=-((x-1/2)^{2}-9/4))
Ensuite on applique l'identité remarquable : a²-b² = (a-b)(a+b)
^{2}-9/4)=-((x-1/2-3/2)*(x-1/2+3/2))=-(x-2)*(x+1))
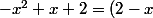*(x+1))
MJoe

-
Antonin
- Membre Naturel
- Messages: 37
- Enregistré le: 25 Aoû 2017, 18:06
-
 par Antonin » 02 Sep 2017, 10:08
par Antonin » 02 Sep 2017, 10:08
Bonjour,
J'ai appris très peu la forme canonique mais si cela reste la manière la plus simple, ayant compris ta démonstration de vais mettre ça!


-
MJoe
- Membre Relatif
- Messages: 295
- Enregistré le: 19 Juil 2017, 06:26
- Localisation: Saint-Nazaire
-
 par MJoe » 02 Sep 2017, 10:42
par MJoe » 02 Sep 2017, 10:42
Tant mieux. Content de voir que le problème est réglé

MJoe.
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 02 Sep 2017, 10:44
par infernaleur » 02 Sep 2017, 10:44
Sinon comme l'énoncé te donne déjà la formule de h(x) il te suffit de développer
(x+1)(-x+2) et tu trouvera bien -x²+x+2 et donc tu peux conclure que c'est la même chose.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
